
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
科目:高中数学 来源: 题型:
【题目】观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
…
问:(1)此表第n行的最后一个数是多少?
(2)此表第n行的各个数之和是多少?
(3)2008是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
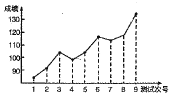
【题目】对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图。下面关于这位同学的数学成绩的分析中,正确的共有( )个。
①该同学的数学成绩总的趋势是在逐步提高;
②该同学在这连续九次测试中的最高分与最低分的差超过40分;
③该同学的数学成绩与考试次号具有比较明显的线性相关性,且为正相关
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的a,b∈R,都有![]() ,且当x>0时,
,且当x>0时,![]()
(1)判断并证明f(x)的单调性;
(2)若f(4)=3,解不等式f(3m2﹣m﹣2)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(附加题)对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的一个不动点.设函数f(x)=ax2+bx+1(a>0).
(Ⅰ)当a=2,b=﹣2时,求f(x)的不动点;
(Ⅱ)若f(x)有两个相异的不动点x1,x2,
(ⅰ)当x1<1<x2时,设f(x)的对称轴为直线x=m,求证:m>![]() ;
;
(ⅱ)若|x1|<2且|x1﹣x2|=2,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )。
A.假设三内角都不大于60度;
B.假设三内角都大于60度;
C.假设三内角至多有一个大于60度;
D.假设三内角至多有两个大于60度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com