
【题目】如图所示,四面体![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中点,且
的中点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)首先利用三角形全等得到![]() ,推导出
,推导出![]() ,利用勾股定理得到
,利用勾股定理得到![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(2)以
;(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,建立空间直角坐标系,利用向量法能求出二面角
轴正方向,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)如图所示,
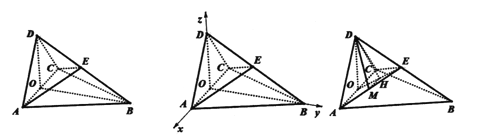
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
由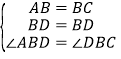 ,得
,得![]() ,所以
,所以![]() ,
,
即![]() 为等腰直角三角形,从而
为等腰直角三角形,从而![]() 为直角,
为直角,
又![]() 为底边
为底边![]() 中点,所以
中点,所以![]() .
.
令![]() ,则
,则![]() ,易得
,易得![]() ,
,
所以![]() ,从而
,从而![]() ,
,
又![]() 为平面
为平面![]() 内两相交直线,
内两相交直线,
所以![]() 平面
平面![]() .
.
(2)由题意可知![]() ,即
,即![]() 到平面
到平面![]() 的距离相等,
的距离相等,
所以点![]() 为
为![]() 的中点,
的中点,
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,建立空间直角坐标系.
轴正方向,建立空间直角坐标系.
设![]() ,则
,则![]() ,
,
易得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则
,则
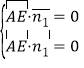 ,取
,取![]() ;
;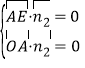 ,取
,取![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,易知
,易知![]() 为锐角,
为锐角,
则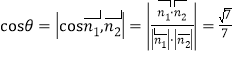 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为![]() ,且各件产品是否为不合格品相互独立.
,且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的![]() 作为
作为![]() 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为![]() ,求
,求![]() ;
;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,点A为曲线
,点A为曲线![]() 上的动点,点B在线段OA的延长线上,且满足
上的动点,点B在线段OA的延长线上,且满足![]() ,点B的轨迹为
,点B的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点C的极坐标为(2,0),求△ABC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两个正整数(允许
是两个正整数(允许![]() 与
与![]() 相等),
相等),![]() 、
、![]() 是两个由若干个实数组成的集合,且
是两个由若干个实数组成的集合,且![]() ,
,![]() (允许
(允许![]() ),集合满足:若
),集合满足:若![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,则或
,则或![]() 且
且![]() ,或
,或![]() (
(![]() 且
且![]() ).定义一个集合
).定义一个集合![]() .试求出
.试求出![]() 的最小可能值(
的最小可能值(![]() 表示集合
表示集合![]() 的元素个数).
的元素个数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)过点
(a>b>0)过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)若斜率为![]() 的直线l与椭圆C交于A,B两点,试探究
的直线l与椭圆C交于A,B两点,试探究![]() 是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
是否为定值?若是定值,则求出此定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标程是
的极坐标程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程
的参数方程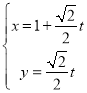 ,(
,(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为曲线
为曲线![]() 上的动点,求三角形
上的动点,求三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com