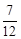甲、乙两人各掷一次骰子(均匀的正方体六个面上分别为l,2,3,4,5,6点)所得点数分别为x,y.
(1)求x<y的概率;
(2)求5<x+y<10的概率.
分析:我们用列举法,易得到甲、乙两人各掷一次骰子,所得的所有基本事件的总数.
(1)我们列出所有的满足x<y的基本事件个数,代入古典概型概率计算公式,即可得到x<y的概率;
(2)再列出所有的满足5<x+y<10的基本事件个数,代入古典概型概率计算公式,即可得到5<x+y<10的概率.
解答:解:记基本事件为(x,y),
则有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3).(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).
共36个基本事件.(2分)
其中满是x<y的基本事件有
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.(5分)
满足5<x+y<10的基本事件有
(1,5),(1,6),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6),(4,2),(4,3).(4,4),(4,5),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),共20个.(8分)
∴(1)x<y的概率
p(x<y)==(10分)
(2)5<x+y<10的概率
P(5<x+y<10)==(12分)
点评:本题考查的知识点是古典概型及其概率计算公式,计算出基本事件总个数及满足条件的基本事件的个数,是解答本题的关键.



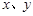 ,则
,则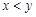 的概率为
的概率为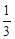 B.
B.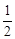 C.
C.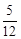 D.
D.