
【题目】已知焦点在y轴上的椭圆E的中心是原点O,离心率等于 ![]() ,以椭圆E的长轴和短轴为对角线的四边形的周长为4
,以椭圆E的长轴和短轴为对角线的四边形的周长为4 ![]() ,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
(Ⅱ)若 ![]() =3
=3 ![]() ,求m2的取值范围.
,求m2的取值范围.
【答案】解:(I)设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0), 由题意可得e=
=1(a>b>0), 由题意可得e= ![]() =
= ![]() ,4
,4 ![]() =4
=4 ![]() ,
,
a2﹣b2=c2 ,
解得a=2,b=1,c= ![]() ,
,
即有椭圆的方程为 ![]() +x2=1;
+x2=1;
(Ⅱ)由题意可得P(0,m),且﹣2<m<2,
设A(x1 , y1),B(x2 , y2),
由 ![]() =3
=3 ![]() ,可得﹣x1=3x2 , ①
,可得﹣x1=3x2 , ①
由直线y=kx+m代入椭圆方程y2+4x2=4,
可得(4+k2)x2+2kmx+m2﹣4=0,
即有x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,②
,②
由①②可得m2= ![]() =1+
=1+ ![]() ,
,
由1+k2≥1,可得0< ![]() ≤3,
≤3,
即有1<m2≤4,由于m∈(﹣2,2),
可得m2的取值范围是(1,4).
【解析】(I)设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),运用离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(Ⅱ)由题意可得P(0,m),且﹣2<m<2,设A(x1 , y1),B(x2 , y2),运用向量共线的坐标表示和直线方程代入椭圆方程,运用韦达定理,可得m2=
=1(a>b>0),运用离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(Ⅱ)由题意可得P(0,m),且﹣2<m<2,设A(x1 , y1),B(x2 , y2),运用向量共线的坐标表示和直线方程代入椭圆方程,运用韦达定理,可得m2= ![]() =1+
=1+ ![]() ,再由不等式的性质,可得所求范围.
,再由不等式的性质,可得所求范围.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1 , ∠BAA1=∠BAC=60°,点O是线段AB的中点. (Ⅰ)证明:BC1∥平面OA1C;
(Ⅱ)若AB=2,A1C= ![]() ,求二面角A﹣BC﹣A1的余弦值.
,求二面角A﹣BC﹣A1的余弦值.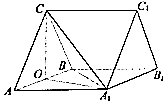
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P(1,0)的直线(不与坐标轴垂直)与椭圆交于A、B两点,设点B关于x轴的对称点为B'.直线AB'与x轴的交点Q是否为定点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: ①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC;⑤平面PBC⊥平面PAC.其中正确命题的序号是 . 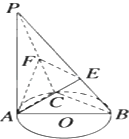
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|2x+a|,a∈R. (Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0﹣2|<3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且Sn= ![]() nan+an﹣c(c是常数,n∈N*),a2=6.
nan+an﹣c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna﹣b(b∈R,a>0且a≠1),e是自然对数的底数.
(1)讨论函数f(x)在(0,+∞)上的单调性;
(2)当a>1时,若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1,求实数a的取值范围.(参考公式:(ax)′=axlna)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com