练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，A为最小角，C为最大角，已知cos(2A+C)=－，sinB=，则cos2(B+C)=__________.


    解析:

    ∵A为最小角∴2A+C=A+A+C＜A+B+C=180°.

    ∵cos(2A+C)=－，∴sin(2A+C)=.

    ∵C为最大角，∴B为锐角，又sinB=. 故cosB=.

    即sin(A+C)=，cos(A+C)=－.

    ∵cos(B+C)=－cosA=－cos［(2A+C)－(A+C)］=－，

    ∴cos2(B+C)=2cos2(B+C)－1=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在不等边△ABC中，a为最大边，如果a2＜b2+c2，则A的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =(cosx，4sinx-2)，
    b
    =(8sinx，2sinx+1)    ，x∈R，设函数f(x)=
    a
    •
    b

    （1）求函数f（x）的最大值；
    （2）在△ABC中，A为锐角，角A，B，C的对边分别为a，b，c，f（A）=6，且△ABC的面积为3，b+c=2+3
    		2
    ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高三数学　苏教版(新课标·2004年初审) 苏教版 题型：022

    在△ABC中，A为最小角，C为最大角，已知cos(2A＋C)＝－，sinB＝，则cos2(B＋C)＝________．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省高三5月模拟考试理科数学 题型：解答题

    三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．）

    16. （本小题满分12分）

    已知向量，定义函数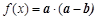

    （Ⅰ）求函数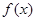最小正周期；

    （Ⅱ）在△ABC中,角A为锐角，且，求边AC的长．

     

     

    查看答案和解析>>

    同步练习册答案