
【题目】如图,四棱锥 ![]() 的底面为正方形,侧面
的底面为正方形,侧面 ![]() 底面
底面 ![]() ,
, ![]() ,
, ![]() 分别为
分别为 ![]() 的中点.
的中点.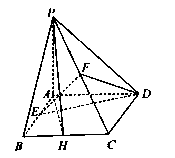
(1)求证: ![]() 面
面 ![]() ;
;
(2)求证:平面 ![]() 平面
平面 ![]() .
.
【答案】
(1)解:取 ![]() 中点
中点 ![]() ,连接
,连接 ![]() ,∵在
,∵在 ![]() 中,
中, ![]() 为中点,
为中点,
∴ ![]() 且
且 ![]() .
.
因为在正方形 ![]() 中,
中, ![]() 且
且 ![]() ,∴
,∴ ![]() 且
且 ![]() ,
,
即四边形 ![]() 为平行四边形,∴
为平行四边形,∴ ![]() ,
,
因为 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() 平面
平面 ![]() .
.
(2)解:∵侧面 ![]() ⊥底面
⊥底面 ![]() ,
, ![]() ,侧面
,侧面 ![]() 底面
底面 ![]() ,
,
∴ ![]() 底面
底面 ![]() ,∵
,∵ ![]() 底面
底面 ![]() ,∴
,∴ ![]() .
.
∵ ![]() 分别为正方形
分别为正方形 ![]() 边
边 ![]() 中点,∴
中点,∴ ![]() ,
,
则 ![]() ,∴
,∴ ![]() ,则
,则 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,∴平面
,∴平面 ![]() 平面
平面 ![]()
【解析】(1)利用平行四边形的性质以及直线与平面平行的判定定理可证明结论。
(2)首先根据已知条件中平面PAD与平面ABCD垂直,得出直线PA与平面ABCD垂直,证明PA与DE垂直;利用平面ABCD内两个三角形相似,证明DE与AE垂直。证明PH与平面PAE垂直,根据平面与平面垂直的判定定理证明结论。


科目:高中数学 来源: 题型:
【题目】某校一模考试数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,可见部分如下
试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在 ![]() 之间的频数;
之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于 ![]() ,
, ![]() ,和
,和 ![]() 分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于
分数段的试卷中抽取8份进行分析,再从中任选2人进行交流,求交流的2名学生中,恰有一名成绩位于 ![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的函数y=(m+6)x2+2(m﹣1)x+m+1恒有零点.
(1)求m的范围;
(2)若函数有两个不同零点,且其倒数之和为﹣4,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击队有8名队员,其中男队员5名,女队员3名,从中随机选3名队员参加射击表演活动.
(1)求选出的3名队员中有一名女队员的概率;
(2)求选出的3名队员中女队员人数比男队员人数多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段 ![]() 的中点,将
的中点,将 ![]() 沿
沿 ![]() 折起,使平面
折起,使平面 ![]() 平面
平面 ![]() ,得到几何体
,得到几何体 ![]() .
.
(1)若 ![]() 分别为线段
分别为线段 ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面 ![]() ;
;
(2)求证: ![]() 平面
平面 ![]() ;
;
(3)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数据3,3,2,3,6,3,10,3,6,3,2.
①这组数据的众数是3;
②这组数据的众数与中位数的数值不相等;
③这组数据的中位数与平均数的数值相等;
④这组数据的平均数与众数的值相等.
其中正确的结论的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com