
分析 可求导数$f′(x)=\frac{a}{x}+x$,而根据题意便可得出f′(x)≥2对于任意x>0都成立,这样便可得出x2-2x+a≥0对任意x∈(0,+∞)恒成立,从而有二次函数y=x2-2x+a的最小值$\frac{4a-4}{4}≥0$,从而可求出a的取值范围.
解答 解:$f′(x)=\frac{a}{x}+x$;
根据$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}≥2$恒成立得:$\frac{a}{x}+x≥2$恒成立;
整理成,x2-2x+a≥0在(0,+∞)上恒成立;
∴$\frac{4a-4}{4}≥0$;
∴a≥1;
∴a的取值范围是[1,+∞).
故答案为:[1,+∞).
点评 考查基本初等函数导数的求法,函数导数的几何意义,直线斜率的计算公式,以及熟悉二次函数的图象.


科目:高中数学 来源: 题型:解答题
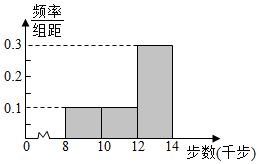 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
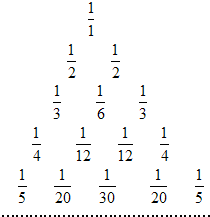 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com