
【题目】如图,四边形![]() 是直角梯形,
是直角梯形, ![]() ,又
,又![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析.(2)![]() .
.
【解析】试题分析:方法1:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)取BC的中点N,连MN.∵![]() ,∴
,∴![]() ,∴
,∴![]() 平面ABC.作
平面ABC.作![]()
![]() ,交AC的延长线于H,连结MH.由三垂线定理得
,交AC的延长线于H,连结MH.由三垂线定理得![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角.∵直线AM与直线PC所成的角为
的平面角.∵直线AM与直线PC所成的角为![]() ,∴在
,∴在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
故二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分
方法2:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.设![]() ,则
,则![]() .
. 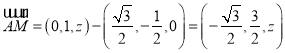 . 5分
. 5分
∵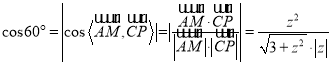 ,
,
且![]() ,∴
,∴![]() ,得
,得![]() ,∴
,∴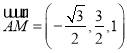 . 8分
. 8分
设平面MAC的一个法向量为![]() ,则由
,则由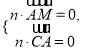 得
得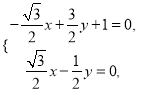 得
得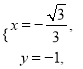 ∴
∴ . 10分
. 10分
平面ABC的一个法向量为![]() .
. 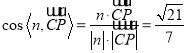 12分
12分
显然,二面角![]() 为锐二面角,∴二面角
为锐二面角,∴二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】学校高一年级开设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选![]() 课程,不选
课程,不选![]() 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中![]() 课程且乙同学未选中
课程且乙同学未选中![]() 课程的概率.
课程的概率.
(Ⅱ)用![]() 表示甲、乙、丙选中
表示甲、乙、丙选中![]() 课程的人数之和,求
课程的人数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018吉林长春高三下学期二模】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如下图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
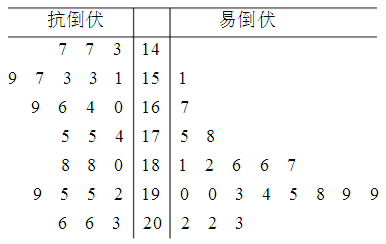
(I)完成列![]() 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(II)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
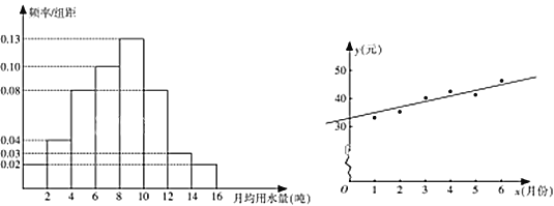
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com