练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
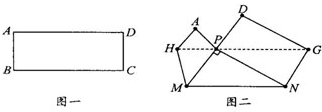
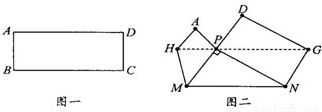
    把图一的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处（如图2），已知∠MPN=90°，PM=3，PN=4，那么矩形纸片ABCD的面积为
    144
    5
    144
    5
    ．
    分析：由勾股定理可求MN，然后可求矩形的宽，最后再利用折叠的性质求出BC的长度，代入矩形的 面积公式可求
    解答：解：由勾股定理可得MN=5
    设Rt△PMN的斜边上的高为h，则矩形的宽AB也为h
    根据直角三角形的面积公式得h=
    PM•PN
    MN
    =
    3×4
    5
    =
    12
    5

    由折叠的性质可得，BC=PM+MN+PN=12
    矩形的面积公AB•BC=
    144
    5

    故答案为：
    144
    5
    点评：本题利用了：折叠的性质：主要思想是一种关于直线的轴对称变换，根据轴对称的性质，及解三角形的基本工具：由勾股定理，及直角三角形和矩形的面积公式求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届河南省分校高一上学期入学考试数学试卷（解析版） 题型：选择题

    有一张矩形纸片ABCD，其中AD=8cm，上面有一个以AD为直径的半圆，正好与对边BC相切．如图（甲）．将它沿DE折叠，使A点落在BC上，如图（乙），这时，半圆还露在外面的部分（阴影部分）的面积是【   】

    A．（π-）cm2                        B．( π-)

    C．（π+）                       D．（π+）

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省仪征市高三第一次涂卡训练数学试卷（解析版） 题型：填空题

    如图，将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点M处，还原后，再沿过点M的直线折叠，使点A落在BC上的点N处，由此可求出的角的正切值是       .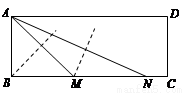

     

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学选修2-1 2.6曲线的方程练习卷（解析版） 题型：解答题

    如图，有一张长为8，宽为4的矩形纸片ABCD，按图示的方向进行折叠，使每次折叠后点B都落在AD边上，此时将B记为B′（图中EF为折痕，点F也可以落在边CD上）．过B′作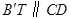交EF于点T，求点T的轨迹方程．

     

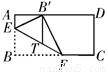
    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年江苏省南京市金陵中学高一实验班选拔考试数学试卷（解析版） 题型：解答题

    把图一的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处（如图2），已知∠MPN=90°，PM=3，PN=4，那么矩形纸片ABCD的面积为    ．

    查看答案和解析>>

    同步练习册答案