Question

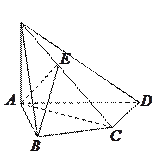
【题目】如图，在四棱锥中， 底面， ， ， 是的中点．

（Ⅰ）证明；

（Ⅱ）证明平面；

（Ⅲ）求二面角的大小．

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析；(Ⅲ) .

【解析】试题分析：

(Ⅰ)由题意可得CD⊥平面PAC，结合线面垂直的定义即可得到AE⊥CD；

(Ⅱ)由题意可得AE⊥PD，AB⊥PD.利用线面垂直的判断定理可得证明平面；

(Ⅲ)由题意找到二面角的平面角，结合三角形的边长关系可得二面角的大小是.

试题解析：

(I)证明：在四棱锥PABCD中，

因PA⊥底面ABCD，CD平面ABCD，故PA⊥CD.

∵AC⊥CD，PA∩AC=A，

∴CD⊥平面PAC.

而AE平面PAC，

∴AE⊥CD.

(II)证明：由PA=AB=BC,∠ABC=60，可得AC=PA.

∵E是PC的中点，∴AE⊥PC.

由(I)知，AE⊥CD，且PC∩CD=C，所以AE⊥平面PCD.

而PD平面PCD，∴AE⊥PD.

∵PA⊥底面ABCD，PD在底面ABCD内射影是AD，AB⊥AD，∴AB⊥PD.

又AB∩AE=A，综上得PD⊥平面ABE.

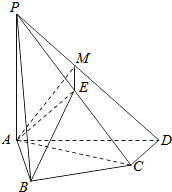
(III)过点A作AM⊥PD，垂足为M，连接EM.

由(II)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则EM⊥PD.

因此∠AME是二面角APDC的平面角。

由已知,得∠CAD=30°.设AC=a,可得 .

在Rt△ADP中,∵AM⊥PD,∴AM.PD=PA.AD.则 .

在Rt△AEM中, .

所以二面角APDC的大小是 .