
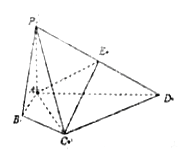
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,先根据线面垂直的性质证明
,先根据线面垂直的性质证明![]() ;进而可得
;进而可得![]() ,再由线面判定定理即可证明
,再由线面判定定理即可证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ;(2)建立空间坐标系,分别求出平面
;(2)建立空间坐标系,分别求出平面![]() 与平面
与平面![]() 的的一个法向量,根据空间向量夹角余弦公式,即可求二面角
的的一个法向量,根据空间向量夹角余弦公式,即可求二面角![]() 的余弦值.
的余弦值.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 又
又![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ;又
;又![]() ,所以
,所以![]() ;
;
又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() .
.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则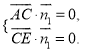 所以
所以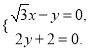
令![]() ,所以
,所以![]() .
.
由(1)知![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
同理![]() ,所以
,所以![]() 平面
平面![]()
所以平面![]() 的一个法向量
的一个法向量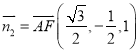 .
.
所以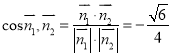 ,
,
由图可知,二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直的判定与性质、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=|ax﹣1|(a∈R),不等式f(x)>5的解集为{x|x<﹣3或x>2}.
(1)求a的值;
(2)解不等式f(x)﹣f( ![]() )≤2.
)≤2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=16.
(1)若a=4,b=5,求cosC的值;
(2)若sinA+sinB=3sinC,且△ABC的面积S=18sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代数学名著《九章算术》中的“盈不足”问题知两鼠穿垣.今有垣厚5尺,两鼠对穿.大鼠日一尺,小鼠亦一尺.大鼠日自倍,小鼠日自半.问:何日相逢?题意是:由垛厚五尺(旧制长度单位, ![]() 尺=
尺= ![]() 寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进
寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进![]() 尺,以后每天的速度为前一天的
尺,以后每天的速度为前一天的![]() 倍;小鼠第一天也打进
倍;小鼠第一天也打进![]() 尺,以后每天的进度是前一天的一半.它们多久可以相遇?
尺,以后每天的进度是前一天的一半.它们多久可以相遇?
A. ![]() 天 B.
天 B. ![]() 天 C.
天 C. ![]() 天 D.
天 D. ![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n.
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有2处错误,请找出错误并予以更正.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,200),[220.240),
[240,260),[260,280),[280,300)分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)在月平均用电量为,[220,240),[240,260),[260,280)的三用户中,用分层抽样的方法抽取10居民,则月平均用电量在[220,240)的用户中应抽取多少户?
(3)求月平均用电量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步雾霾天气现象增多,大气污染危害加重,大气污染可引起心悸,呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(2)已知在患心肺疾病的10位女性中,有3位又患胃病,现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列、数学期望及方差,下面的临界值表供参考:
的分布列、数学期望及方差,下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ,其中
,其中![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com