已知函数f(x)=ax2-bx+1,
(Ⅰ)是否存在实数a,b使f(x)>0的解集是(3,4),若存在,求实数a,b的值,若不存在请说明理由.
(Ⅱ)若a<0,b=a-2,且不等式f(x)≠0在(-2,-1)上恒成立,求a的取值范围.
解:(Ⅰ)不等式ax
2-bx+1>0的解集是(3,4)
故方程ax
2-bx+1=0的两根为3,4,
则是3+4=

,3×4=

∴a=

,b=

而当a=

时,a>0,
不等式ax
2-bx+1>0的解集是(-∞,3)∪(4,+∞)满足要求
故不存在实数a,b使f(x)>0的解集是(3,4).
(II)∵a<0,b=a-2,
∴f(x)=ax
2-(a-2)x+1,
又∵不等式f(x)≠0在(-2,-1)上恒成立,
又∵函数f(x)=ax
2-(a-2)x+1是开口方向朝下,以x=
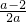

为对称轴的抛物线
∴函数f(x)在(-2,-1)上单调递增
∴f(-2)≥0或f(-1)≤0
解得a<0,所以a∈(-∞,0)(15分)
分析:(I)由已知中f(x)>0的解集是(3,4),我们易根据不等式、函数、方程之间的辩证关系,得到方程ax
2-bx+1=0的两根为3,4,进而根据韦达定理求出满足条件的求出满足实数a,b的值,再结合一元二次不等式解集与系数的关系,得到结论.
(II)根据a<0,b=a-2,我们易判断出函数f(x)图象的形状及在区间(-2,-1)上的单调性,进而根据函数恒成立问题,构造关于a的不等式组,解不等式组,即可得到答案.
点评:本题考查的知识点是一元二次不等式与一元二次方程,二次函数的性质,其中熟练掌握二次函数,一元二次不等式与一元二次方程,之间的转化关系是解答本题的关键.

 ,3×4=
,3×4=
 ,b=
,b=
 时,a>0,
时,a>0,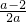
 为对称轴的抛物线
为对称轴的抛物线

 阅读快车系列答案
阅读快车系列答案