已知函数f(x)=(ax2-1)•ex,a∈R.
(Ⅰ)若函数f(x)在x=1时取得极值,求a的值;
(Ⅱ)当a≤0时,求函数f(x)的单调区间.
解:(Ⅰ)f'(x)=(ax
2+2ax-1)•e
x.x∈R…(2分)
依题意得f'(1)=(3a-1)•e=0,解得

.经检验符合题意.…(4分)
(Ⅱ)f'(x)=(ax
2+2ax-1)•e
x,设g(x)=ax
2+2ax-1,
(1)当a=0时,f(x)=-e
x,f(x)在(-∞,+∞)上为单调减函数.…(5分)
(2)当a<0时,方程g(x)=ax
2+2ax-1=0的判别式为△=4a
2+4a,
令△=0,解得a=0(舍去)或a=-1.
1°当a=-1时,g(x)=-x
2-2x-1=-(x+1)
2≤0,
即f'(x)=(ax
2+2ax-1)•e
x≤0,
且f'(x)在x=-1两侧同号,仅在x=-1时等于0,
则f(x)在(-∞,+∞)上为单调减函数.…(7分)
2°当-1<a<0时,△<0,则g(x)=ax
2+2ax-1<0恒成立,
即f'(x)<0恒成立,则f(x)在(-∞,+∞)上为单调减函数.…(9分)
3°a<-1时,△=4a
2+4a>0,令g(x)=0,
方程ax
2+2ax-1=0有两个不相等的实数根
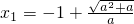
,
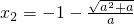
,
作差可知

,
则当
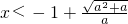
时,g(x)<0,f'(x)<0,f(x)在

上为单调减函数;
当
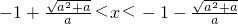
时,g(x)>0,f'(x)>0,f(x)在

上为单调增函数;
当

时,g(x)<0,f'(x)<0,f(x)在
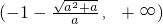
上为单调减函数.…(13分)
综上所述,当-1≤a≤0时,函数f(x)的单调减区间为(-∞,+∞);当a<-1时,函数f(x)的单调减区间为

,
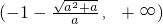
,函数f(x)的单调增区间为

.…(14分)
分析:(I)对函数f(x)进行求导,令导函数在x=1处的值为0,列出方程,求出a,
(II)求出导函数,设g(x)=ax
2+2ax-1,对a的值进行分类讨论结合二次函数的性质研究f′(x);最后令f′(x)>0求出递增区间,令f′(x)<0求出递减区间.
点评:本题考查利用导函数的符号判断函数的单调性、考查函数在某点取得极值的条件、考查等价转化的数学思想方法.

 .经检验符合题意.…(4分)
.经检验符合题意.…(4分)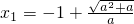 ,
,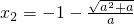 ,
, ,
,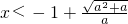 时,g(x)<0,f'(x)<0,f(x)在
时,g(x)<0,f'(x)<0,f(x)在 上为单调减函数;
上为单调减函数;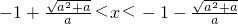 时,g(x)>0,f'(x)>0,f(x)在
时,g(x)>0,f'(x)>0,f(x)在 上为单调增函数;
上为单调增函数; 时,g(x)<0,f'(x)<0,f(x)在
时,g(x)<0,f'(x)<0,f(x)在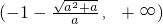 上为单调减函数.…(13分)
上为单调减函数.…(13分) ,
,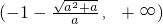 ,函数f(x)的单调增区间为
,函数f(x)的单调增区间为 .…(14分)
.…(14分)
