[题目]我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人.他在中给出一个解不定方程的百鸡问题.问题如下:鸡翁一.值钱五.鸡母一.值钱三.鸡雏三.值钱一．百钱买百鸡.问鸡翁母雏各几何?用代数方法表述为:设鸡翁.鸡母.鸡雏的数量分别为...则鸡翁.鸡母.鸡雏的数量即为方程组的解．其解题过程可用框图表示如下图题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张丘建算经》中给出一个解不定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一．百钱买百鸡，问鸡翁母雏各几何？用代数方法表述为：设鸡翁、鸡母、鸡雏的数量分别为，，，则鸡翁、鸡母、鸡雏的数量即为方程组的解．其解题过程可用框图表示如下图所示，则框图中正整数的值为 ______．

【答案】4

【解析】分析：由得y=25﹣x，结合x=4t，可得框图中正整数m的值．

详解：由得：y=25﹣x，故x必为4的倍数，

当x=4t时，y=25﹣7t，

由y=25﹣7t＞0得：t的最大值为3，

故判断框应填入的是t＜4？，

即m=4，

故答案为：4

点睛: 本题考查的知识点是程序框图，根据已知分析出y与t的关系式及t的取值范围，是解答的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】2019年，随着中国第一款5G手机投入市场，5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析，得到如下规律：每生产手机万台，其总成本为，其中固定成本为800万元，并且每生产1万台的生产成本为1000万元（总成本=固定成本+生产成本），销售收入万元满足

（1）将利润表示为产量万台的函数；

（2）当产量为何值时，公司所获利润最大？最大利润为多少万元？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）当时，求函数的单调区间；

（2）若的负整数解有且只有两个，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

若的定义域为R，求a的取值范围；

若，求的单调区间；

是否存在实数a，使在上为增函数？若存在，求出a的范围；若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知三棱柱ABC－A1B1C1，侧面ABB1A1为菱形，侧面ACC1A1为正方形，侧面ABB1A1⊥侧面ACC1A1．

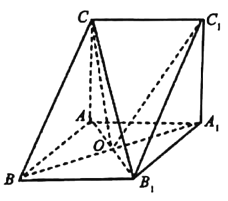
（1）求证：A1B⊥平面AB1C；

（2）若AB＝2，∠ABB1＝60°，求三棱锥C1－COB1的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系中，圆的参数方程为（为参数），以为极点，轴非负半轴为极轴建立极坐标系. 直线的极坐标方程是.

（Ⅰ）求圆的极坐标方程和直线的直角坐标方程；

（Ⅱ）射线与圆的交点为，与直线的交点为，求线段的长.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】北京101中学校园内有一个“少年湖”，湖的两侧有一个音乐教室和一个图书馆，如图，若设音乐教室在A处，图书馆在B处，为测量A，B两地之间的距离，某同学选定了与A，B不共线的C处，构成△ABC，以下是测量的数据的不同方案：①测量∠A，AC，BC；②测量∠A，∠B，BC；③测量∠C，AC，BC；④测量∠A，∠C，∠B. 其中一定能唯一确定A，B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某研究机构对高三学生的记忆力和判断力进行统计分析，得下表数据：

	6	8	10	12
	2	3	5	6

（1）请在图中画出上表数据的散点图；

（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

（3）试根据（2）求出的线性回归方程，预测记忆力为9的同学的判断力．

练习册

高中

初中

小学