
【题目】陕西省洛川地处北纬35°-36°,东经109°,昼夜温差![]() ,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用
,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用![]() (万元)与销售额
(万元)与销售额![]() (万元)之间有下面对应数据:
(万元)之间有下面对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)假设![]() 与
与![]() 之间线性相关,求回归直线方程;
之间线性相关,求回归直线方程;
(2)预测广告和包装费用为10(万元)时销售额是多少?
【答案】(1)![]() ;(2)该果农销售额是82.5万元.
;(2)该果农销售额是82.5万元.
【解析】试题分析:(1)根据表格中的数据分别求出公式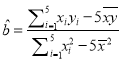 中所需的量,代入公式求出
中所需的量,代入公式求出![]() ,将样本的中心点坐标代入回归方程可得
,将样本的中心点坐标代入回归方程可得![]() ,进而可得结果;(2)
,进而可得结果;(2)![]() 代入(1)中所求回归方程即可得结果.
代入(1)中所求回归方程即可得结果.
试题解析:(1)计算![]() ,
,
 ,
, ![]() ,则回归直线方程是
,则回归直线方程是![]() .
.
(2)当![]() 时,
时, ![]() ,则该果农销售额是82.5万元.
,则该果农销售额是82.5万元.
【方法点晴】本题主要考查线性回归方程及回归分析,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 的中心,点
的中心,点![]() 分别是
分别是![]() 的中点,沿对角线
的中点,沿对角线![]() 把正方形
把正方形![]() 折成二面角
折成二面角![]() .
.
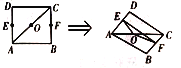
(1)证明:四面体![]() 的外接球的体积为定值,并求出定值;
的外接球的体积为定值,并求出定值;
(2)若二面角![]() 为直二面角,求二面角
为直二面角,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com