
 的图象过点
的图象过点 ,则函数y=f-1(x)-(arcsinx+arccosx)的图象一定过点 .
,则函数y=f-1(x)-(arcsinx+arccosx)的图象一定过点 .  的图象过点
的图象过点 ,代入计算出函数y=f(x)的图象过哪一个点,根据原函数与反函数图象的关系,我们易得函数y=f(x)的反函数y=f-1(x)过什么点,进而得到函数y=f-1(x)-(arcsinx+arccosx)的图象过的定点.
,代入计算出函数y=f(x)的图象过哪一个点,根据原函数与反函数图象的关系,我们易得函数y=f(x)的反函数y=f-1(x)过什么点,进而得到函数y=f-1(x)-(arcsinx+arccosx)的图象过的定点. 的图象过点
的图象过点 ,
, =tan
=tan -f(2)
-f(2)
 )
) ,2)点
,2)点 ,
, .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
| x | 2 |
| x | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() .
.
(I)若![]() ,是否存在a,b
,是否存在a,b![]() R,y=f(x)为偶函数.如果存
R,y=f(x)为偶函数.如果存
在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数![]() 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数![]() 成立.求a的取值范围.
成立.求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(理科)(解析版) 题型:填空题
 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: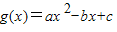 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(文科)(解析版) 题型:填空题
 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)第一次联考数学试卷(理科)(解析版) 题型:填空题
 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com