
分析 (1)f′(x)=12x2+2ax+b.根据函数f(x)=4x3+ax2+bx+5在(-∞,-1)和($\frac{3}{2}$,+∞)单调递增,在(-1,$\frac{3}{2}$)单调递减.可得-1,$\frac{3}{2}$是f′(x)=0的两个实数根.利用根与系数的关系即可得出.
(2)由f′(x)=12x2-6x-18=12(x+1)(x-$\frac{3}{2}$),可知:函数f(x)在[-1,$\frac{3}{2}$)单调递减,函数f(x)在($\frac{3}{2}$,2)上单调递增.进而得出最值.
解答 解:(1)f′(x)=12x2+2ax+b.
∵函数f(x)=4x3+ax2+bx+5在(-∞,-1)和($\frac{3}{2}$,+∞)单调递增,在(-1,$\frac{3}{2}$)单调递减.
∴-1,$\frac{3}{2}$是f′(x)=12x2+2ax+b=0的两个实数根.
∴-1+$\frac{3}{2}$=-$\frac{a}{6}$,-1×$\frac{3}{2}$=$\frac{b}{12}$.
解得a=-3,b=-18.
∴f′(x)=12x2-6x-18=12(x+1)(x-$\frac{3}{2}$),满足条件.
∴f(x)=4x3-3x2-12x+5.
(2)由f′(x)=12x2-6x-18=12(x+1)(x-$\frac{3}{2}$),
可知:函数f(x)在[-1,$\frac{3}{2}$)单调递减,函数f(x)在($\frac{3}{2}$,2)上单调递增.
∴当x=$\frac{3}{2}$时,函数f(x)取得极小值即最小值,$f(\frac{3}{2})$=-$\frac{25}{4}$.
又f(-1)=10,f(2)=1.
∴x=-1时,函数f(x)取得最大值为10.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
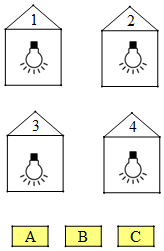 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}≤u≤\sqrt{3}$ | B. | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D. | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y与x成正线性相关关系 | |
| B. | 当商品销售价格提高1元时,商品的销售量减少200件 | |
| C. | 当销售价格为10元/件时,销售量为100件 | |
| D. | 当销售价格为10元/件时,销售量为100件左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,+∞) | B. | ($\frac{3}{2}$,$\frac{25}{8}$) | C. | ($\frac{3}{2}$,$\frac{25}{16}$) | D. | ($\frac{2}{3}$,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,-$\frac{18}{5}$) | B. | ($\frac{4}{3}$,-$\frac{4}{3}$) | C. | (-2,-4) | D. | ($\frac{3}{2}$,-$\frac{6}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com