练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛．若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为，乙获胜的概率为各局比赛结果相互独立．则甲在4局以内（含4局）赢得比赛的概率为（ ）

    A.B.C.D.

    【答案】A

    【解析】

    甲在4局内（含4局）赢得比赛包含3种情况：①甲胜第1、2局；②乙胜第1局，甲胜2、3局；③甲胜第1局，乙胜第2局，甲胜第3、4局，由此可求得甲在4局以内（含4局）赢得比赛的概率.

    由题意，甲在4局内（含4局）赢得比赛包含3种情况：

    ①甲胜第1、2局，概率为；

    ②乙胜第1局，甲胜2、3局，概率为；

    ③甲胜第1局，乙胜第2局，甲胜第3、4局，概率为，

    所以甲在4局以内（含4局）赢得比赛的概率为.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

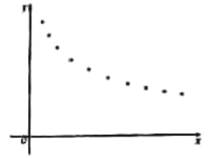
    【题目】某种新产品投放市场一段时间后，经过调研获得了时间（天数）与销售单价（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）.

    1.63

    37.8

    0.89

    5.15

    0.92

    18.40

    表中.

    （1）根据散点图判断，与哪一个更适合作价格关于时间的回归方程类型？（不必说明理由）

    （2）根据判断结果和表中数据，建立关于的回归方程.

    （3）若该产品的日销售量（件）与时间的函数关系为，求该产品投放市场第几天的销售额最高？最高为多少元？

    附：对于一组数据，其回归直线的斜率和截距的最小二乘法估计分别为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，且存在不同的实数x1，x2，x3，使得f（x1）=f（x2）=f（x3），则x1x2x3的取值范围是（　　）

    A. B. C. D.

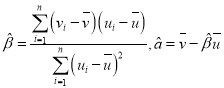    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三角形ABC中，，AC=1，以B为直角顶点作等腰直角三角形BCD（A、D在BC两侧），当∠BAC变化时，线段AD的长度最大值为._______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的离心率是，A、B分别为椭圆的左顶点、上顶点，原点O到AB所在直线的距离为.

    （I）求椭圆C的方程；

    （Ⅱ）已知直线与椭圆相交于不同的两点M，N（均不是长轴的端点），，垂足为H，且，求证：直线恒过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，，，，，，分别为线段，上的点，且，.

    （1）证明：；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间，需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

    以最高气温位于各区间的频率代替最高气温位于该区间的概率.

    （1）求六月份这种酸奶一天的需求量不超过300瓶的概率，；

    （2）设六月份一天销售这种酸奶的利润为(单位:元)，当六月份这种酸奶一天的进货量为450瓶时，写出的所有可能值，并估计大于零的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点为抛物线外一点，过点作抛物线的两条切线，，切点分别为，．

    （Ⅰ）若点为，求直线的方程；

    （Ⅱ）若点为圆上的点，记两切线，的斜率分别为，，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3，从盒中任取3张卡片.

    （1）求所取3张卡片上的数字完全相同的概率;

    （2）表示所取3张卡片上的数字的中位数，求的分布列与数学期望.

    （注：若三个数满足，则称为这三个数的中位数）.

    查看答案和解析>>

    同步练习册答案