
给定椭圆C: +
+ =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”的方程.
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.
①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;
②求证:|MN|为定值.
(1)  +y2=1 x2+y2=4
+y2=1 x2+y2=4
(2) ①y=x+2,y=-x+2 ②见解析
【解析】(1)∵c=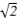 ,a=
,a=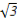 ,∴b=1.
,∴b=1.
∴椭圆方程为 +y2=1,
+y2=1,
准圆方程为x2+y2=4.
(2)①因为准圆x2+y2=4与y轴正半轴的交点为P(0,2),
设过点P(0,2)且与椭圆有一个公共点的直线为y=kx+2,所以由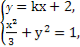 消去y,
消去y,
得(1+3k2)x2+12kx+9=0.
因为椭圆与y=kx+2只有一个公共点,
所以Δ=144k2-4×9(1+3k2)=0,解得k=±1.
所以l1,l2的方程分别为y=x+2,y=-x+2.
②(ⅰ)当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,
则其方程为x=±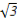 .
.
当l1方程为x=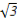 时,
时,
此时l1与准圆交于点(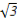 ,1),(
,1),(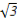 ,-1),
,-1),
此时经过点(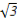 ,1)(或(
,1)(或(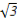 ,-1))且与椭圆只有一个公共点的直线是y=1(或y=-1),
,-1))且与椭圆只有一个公共点的直线是y=1(或y=-1),
即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证l1方程为x=-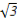 时,直线l1,l2垂直.
时,直线l1,l2垂直.
(ⅱ)当l1,l2都有斜率时,设点P(x0,y0),
其中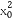 +
+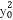 =4.
=4.
设经过点P(x0,y0)与椭圆只有一个公共点的直线为y=t(x-x0)+y0,
则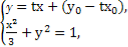 消去y,
消去y,
得(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由Δ=0化简整理得:(3-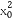 )t2+2x0y0t+1-
)t2+2x0y0t+1-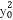 =0.
=0.
因为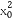 +
+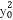 =4,
=4,
所以有(3-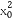 )t2+2x0y0t+(
)t2+2x0y0t+(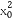 -3)=0.
-3)=0.
设l1,l2的斜率分别为t1,t2,
因为l1,l2与椭圆只有一个公共点,
所以t1,t2满足上述方程(3-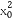 )t2+2x0y0t+(
)t2+2x0y0t+(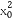 -3)=0,
-3)=0,
所以t1·t2=-1,即l1,l2垂直.
综合(ⅰ)(ⅱ)知:因为l1,l2经过点P(x0,y0),
又分别交其准圆于点M,N,且l1,l2垂直,
所以线段MN为准圆x2+y2=4的直径,
所以|MN|=4.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十四第八章第五节练习卷(解析版) 题型:解答题
已知椭圆C: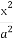 +
+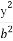 =1(a>b>0).
=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为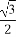 ,求椭圆的标准方程.
,求椭圆的标准方程.
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)过原点O任意作两条互相垂直的直线与椭圆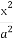 +
+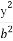 =1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:解答题
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为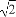 ,且过点P(4,-
,且过点P(4,- ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: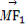 ·
·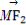 =0.
=0.
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
圆C:x2+y2+2x-2y-2=0的圆心到直线3x+4y+14=0的距离是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第二象限内,则a的取值范围为( )
(A)(-∞,-2) (B)(-∞,-1)
(C)(1,+∞) (D)(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:填空题
设P为椭圆 +
+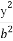 =1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:解答题
已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.

(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:解答题
已知椭圆的中心为坐标原点,短轴长为2,一条准线的方程为l:x=2.
(1)求椭圆的标准方程.
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:选择题
如图,单摆从某点开始来回摆动,离开平衡位置O的距离Scm和时间ts的函数关系式为S=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )

(A)2πs (B)πs (C)0.5s (D)1s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com