
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: 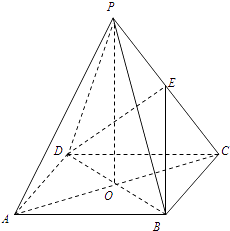
(1)PA∥平面BDE;
(2)BD⊥平面PAC.
【答案】
(1)证明:连接OE,
在△CAP中,CO=OA,CE=EP,
∴PA∥EO,
又∵PA平面BDE,EO平面BDE,
∴PA∥平面BDE.
(2)证明:∵PO⊥底面ABCD,BD平面ABCD,
∴BD⊥PO
又∵四边形ABCD是正方形,
∴BD⊥AC
∵AC∩PO=O,AC,PO平面PAC
∴BD⊥平面PAC
【解析】(1)连接OE,根据三角形中位线定理,可得PA∥EO,进而根据线面平行的判定定理,得到PA∥平面BDE.(2)根据线面垂直的定义,可由PO⊥底面ABCD得到BD⊥PO,结合四边形ABCD是正方形及线面垂直的判定定理可得BD⊥平面PAC
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() ,
, ![]() ,且△ABC的周长为
,且△ABC的周长为 ![]() .
.
(1)求点A的轨迹方程C;
(2)过点P(2,1)作曲线C的一条弦,使弦被这点平分,求此弦所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是函数y=Asin(ωx+φ)(x∈R)在区间 ![]() 上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 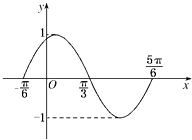
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在定义域内存在实数x0使得f(x0+1)=f(x0)+f(1)成立则称函数f(x)有“溜点x0”
(1)若函数 ![]() 在(0,1)上有“溜点”,求实数m的取值范围;
在(0,1)上有“溜点”,求实数m的取值范围;
(2)若函数f(x)=lg( ![]() )在(0,1)上有“溜点”,求实数a的取值范围.
)在(0,1)上有“溜点”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是首项为0的递增数列,fn(x)=|sin ![]() (x﹣an)|,x∈[an , an+1],n∈N* , 满足:对于任意的b∈[0,1),fn(x)=b总有两个不同的根,则{an}的通项公式为
(x﹣an)|,x∈[an , an+1],n∈N* , 满足:对于任意的b∈[0,1),fn(x)=b总有两个不同的根,则{an}的通项公式为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点G(5,4),圆C1:(x﹣1)2+(y﹣4)2=25,过点G的动直线l与圆C1 , 相交于两点E、F,线段EF的中点为C. (Ⅰ)求点C的轨迹C2的方程;
(Ⅱ)若过点A(1,0)的直线l1:kx﹣y﹣k=0,与C2相交于两点P、Q,线段PQ的中点为M,l1与l2:x+2y+2=0的交点为N,求证:|AM||AN|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ ![]() x+
x+ ![]() ,若数列{bn}满足:b1=1,bn+1=2f(bn)(n∈N*).若对n∈N* , 都M∈Z,使得
,若数列{bn}满足:b1=1,bn+1=2f(bn)(n∈N*).若对n∈N* , 都M∈Z,使得 ![]() <M恒成立,则整数M的最小值是( )
<M恒成立,则整数M的最小值是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月14时的气温,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )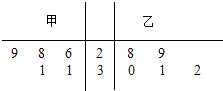
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com