分析:(I)以D为原点,DA、DC、DD
1所在直线分别为x、y、z轴,建立如图所示空间直角坐标系,可得D、A、B、C、A
1、B
1、
C
1、D
1各点的坐标,进而得到向量
、的坐标.设E(0,2,t),由
•=0解出t=1,得到
的坐标,由此得到
•=0且
•=0,从而得到
⊥且
⊥,结合线面垂直判定定理可得A
1C⊥平面BED;
(II)根据
是平面BDE的一个法向量,由空间向量的夹角公式算出
、
夹角的余弦,结合空间直线与平面所成角的定义,可得这个余弦值即为A
1B与平面BDE所成的角的正弦值.
解答:解:( I)如图,以D为原点,DA、DC、DD
1所在直线分别为x、y、z轴,
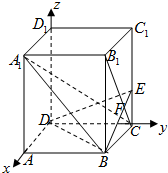
建立空间直角坐标系D-xyz如图所示,可得
D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),
A
1(2,0,4),B
1(2,2,4),C
1(0,2,4),D
1(0,0,4)…(2分)
设E(0,2,t),则
=(-2,0,t),=(-2,0,-4).
∵BE⊥B
1C,
∴可得
•=4+0-4t=0.解之得t=1,
∴E(0,2,1),且
=(-2,0,1).
又∵
=(-2,2,-4),=(2,2,0),…(4分)
∴
•=4+0-4=0且
•=-4+4+0=0…(6分)
∴
⊥且
⊥.
∵BD、BE是平面BDE内的相交直线.
∴
⊥平面BDE…(8分)
(Ⅱ)由(Ⅰ)所建的坐标系,得
=(-2,2,-4)是平面BDE的一个法向量,
又∵
=(0,2,-4),
∴
cos<,>==,
因此,可得A
1B与平面BDE所成角的正弦值为
…(12分)
点评:本题给出正四棱柱,求证线面垂直并求直线与平面所成角的正弦值,着重考查了利用空间向量研究线面垂直、用空间向量的夹角公式求直线与平面所成角等知识,属于中档题.

 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.


 新思维寒假作业系列答案
新思维寒假作业系列答案 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a. 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.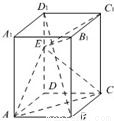 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.