练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设关于x的函数y＝2－2acosx－(2a＋1)的最小值为f(a)．(1)写出f(a)的表达式；(2)试确定能使f(a)＝的a值，并对此时的a，求y的最大值．

    答案：
    解析：

    　　解 (1)y＝2．∵|cosx|≤1，

    　　∴

    　　(2)f(a)＝，1－4a＝，a＝与a≥2矛盾，于是只能有，解得a＝－1．此时有y＝2，当cosx＝1即x＝2kπ(k∈Z)时，＝5．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2007年高考数学理科综合实战演练试卷二 人教版 人教版 题型：044

    解答题

    设关于x的函数y＝2cos2x－2acosx－(2a＋1)的最小值为f(a)．

    (1)

    写出f(a)的表达式；

    (2)

    试确定能使f(a)＝的a的值，并求此时函数y的最大值．

    查看答案和解析>>

    科目：高中数学 来源：江苏省泰州中学2007－2008年度高三第一次月考数学试卷 题型：044

    设关于x的函数y＝－2sin2x－2acosx－2a＋1的最小值为f(a)．

    (1)写出f(a)的表达式；

    (2)试确定能使的a值，并求出此时函数y的最大值．

    查看答案和解析>>

    科目：高中数学 来源：河南省长葛市第三实验高中2011届高三上学期第一次考试理科数学试题 题型：044

    已知函数f(x)＝x＋1，设g1(x)＝f(x)，gn(x)＝f(gn－1(x))(n＞1，n∈N*)

    (1)求g2(x)，g3(x)的表达式，并猜想gn(x)(n∈N*)的表达式(直接写出猜想结果)

    (2)若关于x的函数y＝x2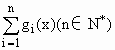＋在区间(－∞，－1]上的最小值为6，求n的值．(符号“”表示求和，例如：＝1＋2＋3＋……＋n)

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2012届高三第一次质量检查数学文科试题 题型：044

    设关于x的函数f(x)＝mx2－(2m2＋4m＋1)x＋(m＋2)lnx，其中m为R上的常数，若函数f(x)在x＝1处取得极大值0．

    (1)求实数m的值；

    (2)若函数f(x)的图像与直线y＝k有两个交点，求实数k的取值范围；

    (3)设函数，若对任意的x∈[1，2]，2f(x)≥g(x)＋4x－2x2恒成立，求实数p的取值范围．

    查看答案和解析>>

    同步练习册答案