练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现有1 000根某品种的棉花纤维，从中随机抽取50根，纤维长度（单位：mm）的数据分组及各组的频数见右上表，据此估计这1 000根中纤维长度不小于37.5 mm的根数是 ．

    纤维长度

    频数

    [22.5，25.5)

    3

    [25.5，28.5)

    8

    [28.5，31.5)

    9

    [31.5，34.5)

    11

    [34.5，37.5)

    10

    [37.5，40.5)

    5

    [40.5，43.5]

    4

    【答案】180
    【解析】解：由图可知，棉花纤维的长度不小于37.5mm段的频率为 ，则1 000根中纤维长度不小于37.5 mm的根数是1000×（0.1+0.08）=180． 故填：180．
    由图分析易得棉花纤维的长度不小于37.5 mm段的频率，根据频率与频数的关系可得1000根棉花纤维中纤维长度不小于37.5mm的根数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=xex ．
    （1）求f（x）的极值；
    （2）k×f（x）≥ x2+x在[﹣1，+∞）上恒成立，求k值的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的部分图象如图所示．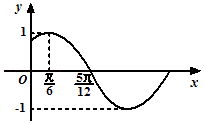

    （1）求函数f（x）的解析式；
    （2）在△ABC中，角A，B，C的对边分别是a，b，c，若（2a﹣c）cosB=bcosC，求 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xoy中，直线的参数方程为 （t为参数），以原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为 ．
    （1）求曲线C的直角坐标方程，并指出其表示何种曲线；
    （2）设直线l与曲线C交于A，B两点，若点P的直角坐标为（1，0），试求当 时，|PA|+|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，城市缺水问题较为突出．某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准x（吨），用水量不超过 x 的部分按平价收费，超出 x 的部分按议价收费．为了了解全市居民用水量的分布情况，通过抽样，获得了 100 位居民某年的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5]分成9组，制成了如图所示的频率分布直方图．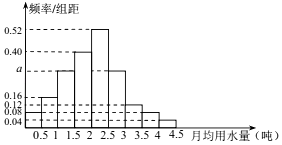

    （Ⅰ）求直方图中 a 的值；
    （Ⅱ）若该市政府希望使 85%的居民每月的用水量不超过标准 x（吨），估计 x 的值，并说明理由；
    （Ⅲ）已知平价收费标准为 4 元/吨，议价收费标准为 8元/吨．当 x=3时，估计该市居民的月平均水费．（同一组中的数据用该组区间的中点值代替）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， ，其中e为自然对数的底数．
    （1）求函数 在x 1处的切线方程；
    （2）若存在 ，使得 成立，其中 为常数，
    求证： ；
    （3）若对任意的 ，不等式 恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， 且a1=a2=1，{nSn+（n+2）an}为等差数列，则a2017= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+x2 ．
    （1）若函数g（x）=f（x）﹣ax在其定义域内为增函数，求实数a的取值范围；
    （2）在（1）的条件下，若a＞1，h（x）=e3x﹣3aexx∈[0，ln2]，求h（x）的极小值；
    （3）设F（x）=2f（x）﹣3x2﹣kx（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且2x0=m+n．问：函数F（x）在点（x0 ， F（x0））处的切线能否平行于x轴？若能，求出该切线方程；若不能，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣a|+m|x+a|． （Ⅰ）当m=a=﹣1时，求不等式f（x）≥x的解集；
    （Ⅱ）不等式f（x）≥2（0＜m＜1）恒成立时，实数a的取值范围是{a|a≤﹣3或a≥3}，求实数m的集合．

    查看答案和解析>>

    同步练习册答案