
【题目】已知函数![]() ,
,![]() ,
,
(1)当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(2)求实数![]() 的取值范围,使
的取值范围,使![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
【答案】(1)![]() 的最大值为37,最小值为1;(2)
的最大值为37,最小值为1;(2)![]() 或
或![]()
【解析】
(1)直接将a=1代入函数解析式,求出最大最小值.
(2)先求f(x)的对称轴x=a,所以若y=f(x)在区间[5,5]上是单调函数,则区间[5,5]在对称轴的一边,所以得到a≤5,或a≥5,这样即得到了a的取值范围.
(1)当a=1时,函数![]() 的对称轴为x=1,
的对称轴为x=1,
∴y=f(x)在区间[5,1]单调递减,在(1,5]单调递增,
且f(5)=37,f(5)=17<37,
∴f(x)min=f(1)=1,f(x)max=f(5)=37;
(2)函数![]() 的图像的对称轴为
的图像的对称轴为![]() ,
,
当![]() ,即
,即![]() 时函数在区间
时函数在区间![]() 上是增加的,
上是增加的,
当![]() ,即
,即![]() 时,函数在区间
时,函数在区间![]() 上是减少的,
上是减少的,
所以使![]() 在区间
在区间![]() 上是单调函数
上是单调函数![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,根据性别分层,采用分层抽样的方法从中抽取100名学生进行调查.
(1)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的100名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),如表是根据调查结果得到的2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选择科目与性别有关?说明你的理由;
(2)在抽取到的女生中按(1)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中随机抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
附参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 。
。
(1)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求乙至多击目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…第八组[190,195],图是按上述分组方法得到的条形图.
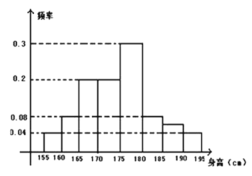
(1)根据已知条件填写将表格填写完整;
组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
样本 | 2 | 4 | 10 | 10 | 15 | 4 |
(2)估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净。假设1千克该蔬菜用清水![]() 千克清洗后,蔬菜上残留的农药为
千克清洗后,蔬菜上残留的农药为![]() 微克,通过样本数据得到
微克,通过样本数据得到![]() 关于
关于![]() 的散点图。由数据分析可用函数
的散点图。由数据分析可用函数![]() 拟合
拟合![]() 与
与![]() 的关系.
的关系.
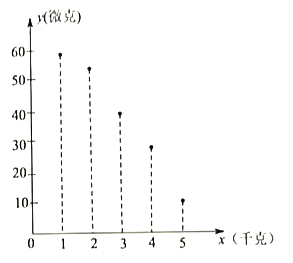
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() (
(![]() 精确到0.1);
精确到0.1);
(2)已知对于残留在蔬菜上的农药,当它的残留量不超过20微克时对人体无害。为了放心食用该蔬菜,请估计至少需要用多少克的清水清洗1千克蔬菜?(答案精确到0.1)
附:①参考数据:![]() ,
,![]() ,
,![]() (其中
(其中![]() ),
),![]() 。
。
②参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).
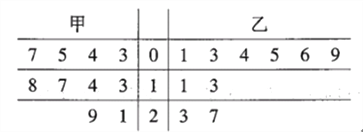
规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com