
【题目】已知椭圆C:![]() 的右焦点F2和上顶点B在直线
的右焦点F2和上顶点B在直线![]() 上,过椭圆右焦点的直线交椭圆于
上,过椭圆右焦点的直线交椭圆于![]() 两点.
两点.
(1)求椭圆C的标准方程;
(2)求![]() 面积的最小值.
面积的最小值.
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在第三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有( )
A.12种B.24种C.36种D.48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .(
.(![]() 且
且![]() )
)
(1)分别判断当![]() 及
及![]() 时函数的奇偶性;
时函数的奇偶性;
(2)在![]() 且
且![]() 的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
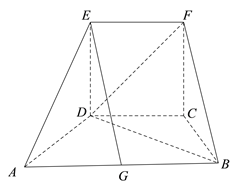
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在区间
,若存在区间![]() 使得
使得![]() :
:
(Ⅰ)![]() 在
在![]() 上是单调函数;
上是单调函数;
(Ⅱ)![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
则称区间![]() 为函数
为函数![]() 的“倍值区间”.
的“倍值区间”.
下列函数中存在“倍值区间”的有______________(填上所有你认为正确的序号)
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米,该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元平方米):
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根据表格数据,完成下列茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数;
A户型 | B户型 | |
2. | ||
3. | ||
4. |
(2)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会,小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格,为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
B.设![]() ,且
,且![]() ,则
,则![]()
C.在残差图中,残差点分布的带状区域的宽带越狭窄,其模型拟合的精度越高
D.已知变量x和y满足关系![]() ,变量y与z正相关,则x与z负相关
,变量y与z正相关,则x与z负相关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com