
【题目】已知数列![]() 和
和![]() 满足
满足![]() 若
若![]() 为等比数列,且
为等比数列,且![]()
(1)求![]() 和
和![]() ;
;
(2)设![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]()
①求![]() ;
;
②求正整数 k,使得对任意![]() 均有
均有![]() .
.
【答案】(1)an=2n(n∈N*).bn=n(n+1)(n∈N*).(2)(i) Sn=![]() (n∈N*).(ii)k=4.
(n∈N*).(ii)k=4.
【解析】解:(1)由题意a1a2a3…an=![]() ,b3-b2=6,知a3=(
,b3-b2=6,知a3=(![]() )b3-b2=8. 设数列{an}的公比为q,又由a1=2,得
)b3-b2=8. 设数列{an}的公比为q,又由a1=2,得![]() ,q=2(q=-2舍去),所以数列{an}的通项为an=2n(n∈N*).
,q=2(q=-2舍去),所以数列{an}的通项为an=2n(n∈N*).
所以,a1a2a3…an=2![]() =(
=(![]() )n(n+1).
)n(n+1).
故数列{bn}的通项为bn=n(n+1)(n∈N*).
(2)(i)由(1)知cn=![]() (n∈N*).所以Sn=
(n∈N*).所以Sn=![]() (n∈N*).
(n∈N*).
(ii)因为c1=0,c2>0,c3>0,c4>0,当n≥5时,cn=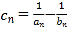
而![]() 得
得![]() 所以,当n≥5时,cn<0.
所以,当n≥5时,cn<0.
综上,若对任意n∈N*恒有Sk≥Sn,则k=4.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过![]() 、
、![]() ,圆心
,圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 交圆相交于
交圆相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)(i)请问![]() 是否为定值.若是,请求出该定值,若不是,请说明理由;
是否为定值.若是,请求出该定值,若不是,请说明理由;
(ii)若![]() 为坐标原点,且
为坐标原点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
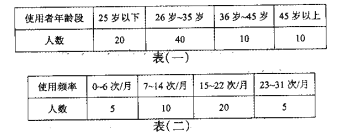
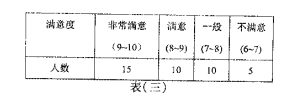
【题目】共享单车入住泉州一周年以来,因其“绿色出行,低碳环保”的理念而备受人们的喜爱,值此周年之际,某机构为了了解共享单车使用者的年龄段,使用频率、满意度等三个方面的信息,在全市范围内发放![]() 份调查问卷,回收到有效问卷
份调查问卷,回收到有效问卷![]() 份,现从中随机抽取
份,现从中随机抽取![]() 份,分别对使用者的年龄段、
份,分别对使用者的年龄段、![]() ~
~![]() 岁使用者的使用频率、
岁使用者的使用频率、![]() ~
~![]() 岁使用者的满意度进行汇总,得到如下三个表格:
岁使用者的满意度进行汇总,得到如下三个表格:
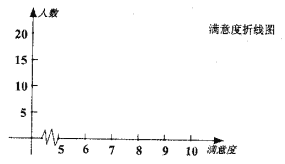
(Ⅰ)依据上述表格完成下列三个统计图形:

(Ⅱ)某城区现有常住人口![]() 万,请用样本估计总体的思想,试估计年龄在
万,请用样本估计总体的思想,试估计年龄在![]() 岁~
岁~![]() 岁之间,每月使用共享单车在
岁之间,每月使用共享单车在![]() ~
~![]() 次的人数.
次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ) ![]() 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)﹣cos2x,求函数g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的公差为d,前n项和为Sn , 等比数列{bn}的公比为q,已知b1=a1 , b2=2,q=d,S10=100.
(1)求数列{an},{bn}的通项公式
(2)当d>1时,记cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙O:x2+y2=1和点M(4,2).
(Ⅰ)过点M向⊙O引切线l,求直线l的方程;
(Ⅱ)求以点M为圆心,且被直线y=2x﹣1截得的弦长为4的⊙M的方程;
(Ⅲ)设P为(Ⅱ)中⊙M上任一点,过点P向⊙O引切线,切点为Q.试探究:平面内是否存在一定点R,使得 ![]() 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com