
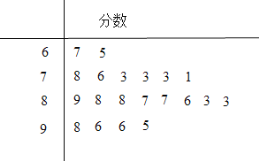
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).
科目:高中数学 来源: 题型:
【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)调查组从该样本的城镇居民中按分层抽样抽取出7人,参加一次阅读交流活动,若活动主办方从这7位居民中随机选取2人作交流发言,求被选中的2位居民都是经常阅读居民的概率.
附: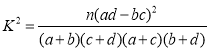 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD是边长为2的正方形,且
的底面ABCD是边长为2的正方形,且![]() .若四棱锥P-ABCD的五个顶点在以4为半径的同一球面上,当PA最长时,则
.若四棱锥P-ABCD的五个顶点在以4为半径的同一球面上,当PA最长时,则![]() ______________;四棱锥P-ABCD的体积为______________.
______________;四棱锥P-ABCD的体积为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 右顶点为
右顶点为![]() 过右焦点且垂直于
过右焦点且垂直于![]() 轴的直线与椭圆相交于
轴的直线与椭圆相交于![]() 两点,所得四边形
两点,所得四边形![]() 为菱形,且其面积为
为菱形,且其面积为![]() .
.
(1)求椭圆的方程;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,试求三角形
两点,试求三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com