
函数的单调性和奇偶性是函数的两个重要性质,你能说说这两条性质的区别吗?函数的奇偶性反映在函数图象上表现为图象的对称性,你能说出奇偶性与对称性之间的对应关系吗?用定义来判断函数的奇偶性的一般步骤是什么?请你总结一下函数的奇偶性的性质.
|
根据函数单调性和奇偶性的定义我们知道:函数的单调性反映函数值的变化趋势,反映在图象上,是曲线的上升或下降.它通过定义区间(或子区间)内的任意两点x1、x2所对应的函数值大小的比较,推断定义区间(或其子区间)内无限多个函数值间的大小关系;函数的奇偶性反映函数的整体形态,即函数的奇偶性是函数图象对称性的代数描述. 奇函数的图象关于原点成中心对称图形,偶函数的图象关于y轴成轴对称图形;反之也成立.所以可用函数图象的对称性来判断函数的奇偶性. 判断函数奇偶性的一般方法是利用定义,通常是先求函数的定义域,观察定义域是否关于原点对称,然后验证f(-x)是否等于±f(x);有时也可利用定义的变形形式,如验证f(-x)±f(x)=0,或 函数奇偶性的几个性质: (1)对称性:奇偶函数的定义域关于原点对称; (2)整体性:奇偶性是函数的整体性质,对定义域内任意一个x都必须成立; (3)可逆性:f(-x)=f(x) (4)等价性:f(-x)=f(x) (5)奇函数的图象关于原点对称,偶函数的图象关于y轴对称; (6)可分性:根据奇偶性可将函数分为四类:奇函数,偶函数,既是奇函数又是偶函数,非奇非偶函数. |


科目:高中数学 来源: 题型:
| 3 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
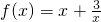
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数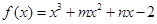 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数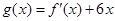 的图象关于y轴对称.
的图象关于y轴对称.
(1)求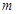 、
、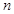 的值及函数
的值及函数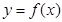 的单调区间;
的单调区间;
(2)若函数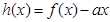 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数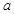 的取值范围。
的取值范围。
【解析】本试题主要考查了导数在函数研究中的应用。利用导数能求解函数的单调性和奇偶性问题,以及能根据函数单调区间,逆向求解参数的取值范围的求解问题。要利用导数恒小于等于零来解得 。
查看答案和解析>>
科目:高中数学 来源:新课标高三数学抛物线、直线与圆锥曲线的位置关系专项训练(河北) 题型:解答题
已知函数 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数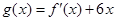 的图象关于y轴对称.
的图象关于y轴对称.
(1)求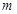 、
、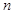 的值及函数
的值及函数 的单调区间;
的单调区间;
(2)若函数 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数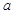 的取值范围。
的取值范围。
【解析】本试题主要考查了导数在函数研究中的应用。利用导数能求解函数的单调性和奇偶性问题,以及能根据函数单调区间,逆向求解参数的取值范围的求解问题。要利用导数恒小于等于零来解得 。
查看答案和解析>>
科目:高中数学 来源:安徽省蚌埠二中2013届高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数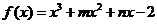 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数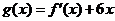 的图象关于y轴对称.
的图象关于y轴对称.
(1)求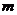 、
、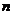 的值及函数
的值及函数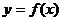 的单调区间;
的单调区间;
(2)若函数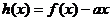 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数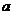 的取值范围。
的取值范围。
【解析】本试题主要考查了导数在函数研究中的应用。利用导数能求解函数的单调性和奇偶性问题,以及能根据函数单调区间,逆向求解参数的取值范围的求解问题。要利用导数恒小于等于零来解得 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com