
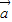 与
与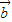 共线,则存在唯一的实数λ,使
共线,则存在唯一的实数λ,使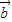 =λ
=λ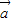 ;
;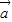 、
、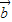 、
、 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;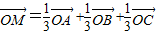 ,则点M一定在平面ABC上,且在△ABC内部.
,则点M一定在平面ABC上,且在△ABC内部.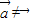 这一条件缺少,于是①错.
这一条件缺少,于是①错.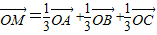 两边同加
两边同加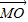 ,
, (
(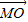 +
+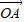 )+
)+ (
(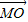 +
+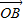 )+
)+ (
(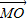 +
+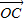 )=
)=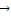 ,
, +
+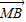 +
+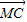 =
=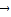 ,
,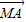 =-(
=-(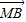 +
+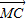 )则
)则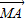 、
、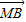 、
、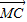 共面,
共面,

科目:高中数学 来源:2014届四川省攀枝花市高二上学期期中理科数学试卷(解析版) 题型:填空题
下列命题:①若 与
与 共线,则存在唯一的实数
共线,则存在唯一的实数 ,使
,使 =
=
 ;
;
②空间中,向量 、
、 、
、 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③P是△ABC所在平面外一点,O是点P在平面 上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.
上的射影.若PA 、PB、PC两两垂直,则O是△ABC垂心.
④若 三点不共线,
三点不共线, 是平面
是平面 外一点.
外一点. ,则点
,则点 一定在平面
一定在平面 上,且在△ABC内部,上述命题中正确的命题是
.
上,且在△ABC内部,上述命题中正确的命题是
.
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高一下学期期中联考数学试卷(解析版) 题型:选择题
给出下列命题:
①向量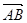 与
与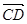 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
②两个单位向量是相等向量;
③若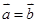 ,
, 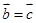 ,则
,则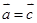 ;
;
④若一个向量的模为0,则该向量的方向不确定;
⑤若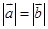 ,则
,则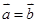 。
。
⑥若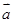 与
与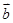 共线,
共线, 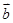 与
与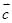 共线,则
共线,则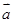 与
与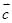 共线
共线
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三第二次月考理科数学试卷 题型:选择题
给出下列命题:①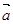 ·
·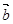 =0,则
=0,则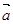 =
=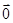 或
或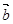 =
=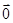 .
.
②若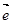 为单位向量且
为单位向量且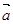 //
//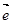 ,则
,则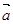 =|
=|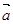 |·
|·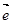 .
.
③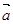 ·
·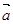 ·
·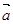 =|
=|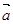 |3.
|3.
④若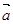 与
与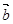 共线,
共线,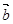 与
与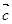 共线,则
共线,则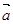 与
与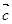 共线.其中正确的个数是:
共线.其中正确的个数是:
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014届福建省晋江市高一上学期期末考试数学 题型:填空题
设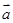 与
与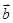 为非零向量,下列命题:
为非零向量,下列命题:
①若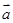 与
与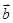 平行,则
平行,则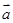 与
与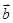 向量的方向相同或相反;
向量的方向相同或相反;
②若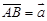 ,
,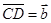 ,
,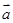 与
与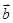 共线,则A、B、C、D四点必在同一条直线上;
共线,则A、B、C、D四点必在同一条直线上;
③若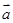 与
与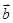 共线,则
共线,则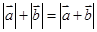 ;
;
④若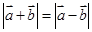 ,则
,则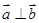 ;
;
⑤若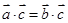 ,
,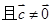 ,则
,则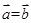
其中正确的命题的编号是 (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试8-理科-立体几何初步、空间向量与立体几何 题型:填空题
下列命题:
①若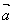 与
与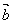 共线,
共线, 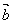 与
与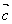 共线,则
共线,则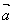 与
与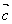 共线;
共线;
②向量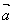 、
、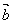 、
、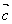 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③若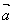 与
与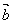 共线,则存在唯一的实数
共线,则存在唯一的实数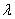 ,使
,使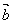 =
=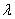
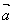 ;
;
④若A、B、C三点不共线,0是平面ABC外一点.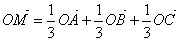 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,
上述命题中的真命题是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com