
【题目】已知函数![]() ,其定义域为
,其定义域为![]() .(其中常数
.(其中常数![]() ,是自然对数的底数)
,是自然对数的底数)
(1)求函数![]() 的递增区间;
的递增区间;
(2)若函数![]() 为定义域上的增函数,且
为定义域上的增函数,且![]() ,证明:
,证明: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)求得函数的导数![]() ,分类讨论,即可求解函数的单调区间;
,分类讨论,即可求解函数的单调区间;
(2)由题意,问题转化为![]() ,令
,令![]() ,
,![]() ,
,
即证![]() ,根据函数的单调性,即可作出证明.
,根据函数的单调性,即可作出证明.
(1)易知![]() ,
,
①若![]() ,由
,由![]() 解得
解得![]() ,∴函数
,∴函数![]() 的递增区间为
的递增区间为![]() ;
;
②若![]() ,则
,则
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴函数![]() 的递增区间为
的递增区间为![]() 和
和![]() ;
;
③若![]() ,则
,则![]() ,∴函数
,∴函数![]() 的递增区间为
的递增区间为![]() ;
;
④若![]() ,则
,则
|
| 1 |
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴函数![]() 的递增区间为
的递增区间为![]() 和
和![]() ;
;
综上,若![]() ,
,![]() 的递增区间为
的递增区间为![]() ;
;
若![]() ,
,![]() 的递增区间为
的递增区间为![]() 和
和![]() ;
;
若![]() ,函数
,函数![]() 的递增区间为
的递增区间为![]() ;
;
若![]() ,函数
,函数![]() 的递增区间为
的递增区间为![]() 和
和![]() .
.
(2)∵函数![]() 为
为![]() 上的增函数,∴
上的增函数,∴![]() ,即
,即![]() ,
,
注意到![]() ,故
,故![]() ,
,
∴不妨设![]() ,
,
欲证![]() ,只需证
,只需证![]() ,只需证
,只需证![]() ,
,
即证![]() ,即证
,即证![]() ,
,
令![]() ,
,![]() ,只需证
,只需证![]() ,
,
∴![]()
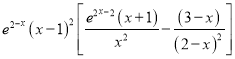 ,
,
下证![]() ,即证
,即证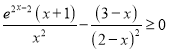 ,
,
由熟知的不等式![]() 可知
可知![]() ,
,
当![]() 时,即
时,即![]() ,
,
∴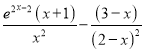
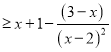
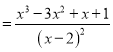 ,
,
易知当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴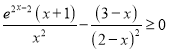 ,
,
∴![]() ,即
,即![]() 单调递增,即
单调递增,即![]() ,从而
,从而![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的![]() 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产![]() 部件的人数为
部件的人数为![]() ,分别写出完成
,分别写出完成![]() 三种部件生产需要的时间;
三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球的公转轨道可以看作是以太阳为一个焦点的椭圆,根据开普勒行星运动第二定律,可知太阳和地球的连线在相等的时间内扫过相等的面积,某同学结合物理和地理知识得到以下结论:①地球到太阳的距离取得最小值和最大值时,地球分别位于图中![]() 点和
点和![]() 点;②已知地球公转轨道的长半轴长约为
点;②已知地球公转轨道的长半轴长约为![]() 千米,短半轴长约为
千米,短半轴长约为![]() 千米,则该椭圆的离心率约为
千米,则该椭圆的离心率约为![]() .因此该椭圆近似于圆形:③已知我国每逢春分(
.因此该椭圆近似于圆形:③已知我国每逢春分(![]() 月
月![]() 日前后)和秋分(
日前后)和秋分(![]() 月
月![]() 日前后),地球会分别运行至图中
日前后),地球会分别运行至图中![]() 点和
点和![]() 点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
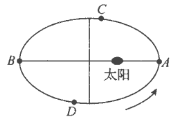
A.①B.①②C.②③D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com