
【题目】已知可导函数f(x)的定义域为![]() ,且满足
,且满足![]() ,
,![]() ,则对任意的
,则对任意的![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() .
.
(Ⅰ)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(Ⅱ)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求四棱锥
,求四棱锥![]() 体积的最大值.
体积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士数学家、物理学家欧拉发现任一凸多面体(即多面体内任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数V.棱数E及面数F满足等式![]() ,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮、简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,它是由m块黑色正五边形面料和
,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮、简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,它是由m块黑色正五边形面料和![]() 块白色正六边形面料构成的.则
块白色正六边形面料构成的.则![]() ( )
( )

A.20B.18C.14D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知可导函数f(x)的定义域为![]() ,且满足
,且满足![]() ,
,![]() ,则对任意的
,则对任意的![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产能利用率是工业总产出对生产设备的比率,反映了实际生产能力到底有多少在运转发挥生产作用.汽车制造业的产能利用率的正常值区间为![]() ,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
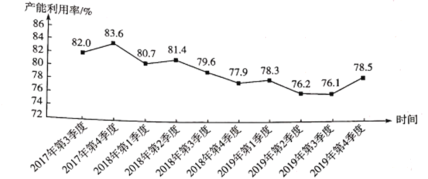
A.10个季度中,汽车产能利用率低于“安全线”的季度有5个
B.10个季度中,汽车产能利用率的中位数为![]()
C.2018年4个季度的汽车产能利用率的平均数为![]()
D.与上一季度相比,汽车产能利用率变化最大的是2019年第4季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为( )(参考数据![]() )
)
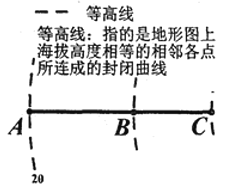
A.30米B.50米C.60米D.70米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com