
【题目】某校从参加高三模拟考试的学生中随机抽取![]() 名学生,将其数学成绩(均为整数)分成六段
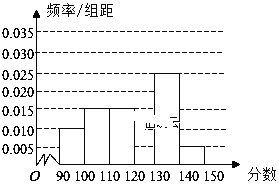
名学生,将其数学成绩(均为整数)分成六段![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在![]() 内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
(2)用分层抽样的方法,在分数段为![]() 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段![]() 内的概率
内的概率
【答案】(1)详见解析(2)![]()
【解析】
(1)首先可以计算出除了![]() 之外的其他分数段的频率,然后计算出分数在
之外的其他分数段的频率,然后计算出分数在![]() 内的频率,再用频率除以组距即可,然后用每一分数段的中间数乘以每一分数段的概率再相加即可得出平均分;
内的频率,再用频率除以组距即可,然后用每一分数段的中间数乘以每一分数段的概率再相加即可得出平均分;
(2)首先算出在![]() 以及
以及![]() 两个分数段中抽取的人数,然后列出从中任取2个的所有可能的事件,并找出满足题目要求的事件,即可得出结果。
两个分数段中抽取的人数,然后列出从中任取2个的所有可能的事件,并找出满足题目要求的事件,即可得出结果。
(1)分数在![]() 内的频率为
内的频率为![]() ,
,![]() (直方图略),平均分为:
(直方图略),平均分为:![]() ,
,
(2)由题意,![]() 分数段的人数为:
分数段的人数为:![]() 人,
人,
![]() 分数段的人数为:
分数段的人数为:![]() 人,
人,
因为用分层抽样的方法在分数段为![]() 的学生中抽取一个容量为
的学生中抽取一个容量为![]() 的样本,抽样比
的样本,抽样比![]() ,所以需在
,所以需在![]() 分数段内抽取
分数段内抽取![]() 人,并分别记为
人,并分别记为![]() ;
;
在![]() 分数段内抽取
分数段内抽取![]() 人并分别记为
人并分别记为![]() ;
;
设“从样本中任取2人,至多有1人在分数段![]() 内”为事件A,
内”为事件A,
则基本事件有:![]()
![]() 共15种.
共15种.
事件A包含的基本事件有:(![]()
![]() 共
共![]() 种,所以
种,所以![]() 。
。


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )
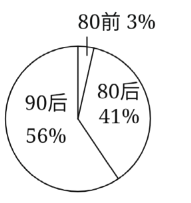
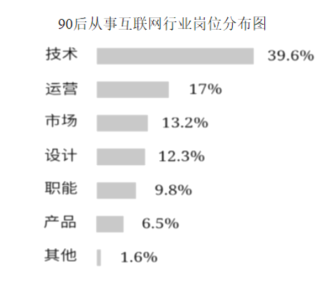
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80后多
D.互联网行业中从事运营岗位的人数90后比80前多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ,
,![]() ,
,![]() ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发〔2016〕74号)的要求,到2020年,全国二氧化硫排放总量要控制在1580万吨以内,要比2015年下降15%.假设“十三五”期间每一年二氧化硫排放总量下降的百分比都相等,2015年后第![]() 年的二氧化硫律放总量最大值为
年的二氧化硫律放总量最大值为![]() 万吨.
万吨.
(1)求![]() 的解析式;
的解析式;
(2)求2019年全国二氧化赖持放总量要控制在多少万晚以内(精确到1万吨).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
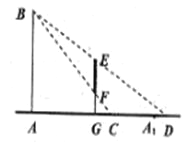
,![]() ,顾客可视的镜像范围为
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com