
【题目】已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() ;
;
(Ⅱ)向量![]() ,
,![]() ,若函数
,若函数![]() 的图象关于直线
的图象关于直线![]() 对称,求角
对称,求角![]() 、
、![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为x元/千克,政府补贴为t元/千克,根据市场调查,当16≤x≤24时,这种食品市场日供应量p万千克与市场日需求量q万千克近似地满足关系:p=2(x+4t-14)(x≥16,t≥0),q=24+8ln ![]() (16≤x≤24).当p=q时的市场价格称为市场平衡价格.
(16≤x≤24).当p=q时的市场价格称为市场平衡价格.
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域.
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(![]() ,
,![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 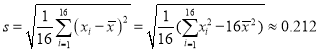 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图.
(2)求回归方程.
(3)试预测广告费支出为10百万元时,销售额多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,直线
,直线![]() :
: ![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆
的短半轴长为半径的圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,与圆
,与圆![]() 相交于两点
相交于两点![]() ,
, ![]() ,若
,若![]() 是钝角三角形,求直线
是钝角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com