
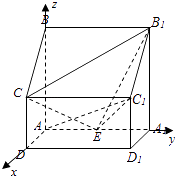
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 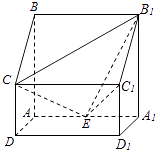
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
【答案】
(1)证明:以点A为原点建立空间直角坐标系,如图,
依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).
则 ![]() ,
,
而 ![]() =0.
=0.
所以B1C1⊥CE;
(2)解: ![]() ,
,
设平面B1CE的法向量为 ![]() ,
,
则 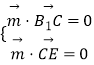 ,即
,即 ![]() ,取z=1,得x=﹣3,y=﹣2.
,取z=1,得x=﹣3,y=﹣2.
所以 ![]() .
.
由(1)知B1C1⊥CE,又CC1⊥B1C1,所以B1C1⊥平面CEC1,
故 ![]() 为平面CEC1的一个法向量,
为平面CEC1的一个法向量,
于是 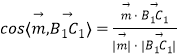 =
= ![]() .
.
从而 ![]() =
= ![]() =
= ![]() .
.
所以二面角B1﹣CE﹣C1的正弦值为 ![]() .
.
(3)解: ![]() ,
,
设 ![]() 0≤λ≤1,
0≤λ≤1,
有 ![]() .
.
取 ![]() 为平面ADD1A1的一个法向量,
为平面ADD1A1的一个法向量,
设θ为直线AM与平面ADD1A1所成的角,
则 ![]() =
= 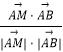
= ![]() .
.
于是 ![]() .
.
解得 ![]() .所以
.所以 ![]() .
.
所以线段AM的长为 ![]() .
.
【解析】(1)由题意可知,AD,AB,AA1两两互相垂直,以a为坐标原点建立空间直角坐标系,标出点的坐标后,求出 ![]() 和
和 ![]() ,由
,由 ![]() 得到B1C1⊥CE;(2)求出平面B1CE和平面CEC1的一个法向量,先求出两法向量所成角的余弦值,利用同角三角函数基本关系求出其正弦值,则二面角B1﹣CE﹣C1的正弦值可求;(3)利用共线向量基本定理把M的坐标用E和C1的坐标及待求系数λ表示,求出平面ADD1A1的一个法向量,利用向量求线面角的公式求出直线AM与平面ADD1A1所成角的正弦值,代入
得到B1C1⊥CE;(2)求出平面B1CE和平面CEC1的一个法向量,先求出两法向量所成角的余弦值,利用同角三角函数基本关系求出其正弦值,则二面角B1﹣CE﹣C1的正弦值可求;(3)利用共线向量基本定理把M的坐标用E和C1的坐标及待求系数λ表示,求出平面ADD1A1的一个法向量,利用向量求线面角的公式求出直线AM与平面ADD1A1所成角的正弦值,代入 ![]() 求出λ的值,则线段AM的长可求.
求出λ的值,则线段AM的长可求.
【考点精析】通过灵活运用直线与平面垂直的性质和空间角的异面直线所成的角,掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则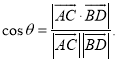 即可以解答此题.
即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下结论正确的序号有_________
(1)根据![]() 列联表中的数据计算得出
列联表中的数据计算得出![]() ≥6.635, 而P(
≥6.635, 而P(![]() ≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
(2)在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
(3)在线性回归分析中,相关系数为![]() ,
,![]() 越接近于1,相关程度越大;
越接近于1,相关程度越大;![]() 越小,相关程度越小.
越小,相关程度越小.
(4)在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的16%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金y(单位:万元),销售利润x(单位:万元)
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老张获得5.6万元的奖金,那么他的销售利润是多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com