
°æƒø°øƒ≥∏ğøĞÀƵƒ…Ó∂»![]() « ±º‰
« ±º‰![]() £¨µ•Œª£∫
£¨µ•Œª£∫ ![]() µƒ∫Ø ˝£¨º«◊˜
µƒ∫Ø ˝£¨º«◊˜![]() .œ¬√Ê «ƒ≥»’ÀÆ…Óµƒ ˝æı£∫
.œ¬√Ê «ƒ≥»’ÀÆ…Óµƒ ˝æı£∫

æ≠≥§∆Ğπğ≤Ï£¨ ![]() µƒ«˙œşø…“‘Ω¸À∆µÿø¥≥…∫Ø ˝
µƒ«˙œşø…“‘Ω¸À∆µÿø¥≥…∫Ø ˝![]() µƒÕºœÛ.“ª∞„«Èøˆœ¬£¨¥¨≤∞∫Ω–– ±£¨¥¨µ◊¿Î∫£µ◊µƒæ‡¿ÎŒ™
µƒÕºœÛ.“ª∞„«Èøˆœ¬£¨¥¨≤∞∫Ω–– ±£¨¥¨µ◊¿Î∫£µ◊µƒæ‡¿ÎŒ™![]() ªÚ
ªÚ![]() “‘…œ ±»œŒ™ «∞≤»´µƒ£®¥¨≤∞Õ£øø ±£¨¥¨µ◊÷ª–Ë≤ª≈ˆ∫£µ◊º¥ø…£©.
“‘…œ ±»œŒ™ «∞≤»´µƒ£®¥¨≤∞Õ£øø ±£¨¥¨µ◊÷ª–Ë≤ª≈ˆ∫£µ◊º¥ø…£©.
£®1£©«Û![]() ”Î
”Î![]() ¬˙◊„µƒ∫Ø ˝πÿœµ Ω£ª
¬˙◊„µƒ∫Ø ˝πÿœµ Ω£ª
£®2£©ƒ≥¥¨≥‘ÀÆ≥Ã∂»£®¥¨µ◊¿ÎÀÆ√ʵƒæ‡¿Î£©Œ™![]() £¨»Áπ˚∏√¥¨œ£Õ˚‘ĞÕ¨“ªÃσĞ∞≤»´Ω¯≥ˆ∏𣨫Ό À¸Õ¨“ªÃσĞ◊Ó∂‡ƒİ‘Ğ∏ğƒĞÕ£¡Ù∂‡…Ÿ–° ±£ø£®∫ˆ¬‘Ω¯≥ˆ∏ğÀ˘–˵ƒ ±º‰£©.
£¨»Áπ˚∏√¥¨œ£Õ˚‘ĞÕ¨“ªÃσĞ∞≤»´Ω¯≥ˆ∏𣨫Ό À¸Õ¨“ªÃσĞ◊Ó∂‡ƒİ‘Ğ∏ğƒĞÕ£¡Ù∂‡…Ÿ–° ±£ø£®∫ˆ¬‘Ω¯≥ˆ∏ğÀ˘–˵ƒ ±º‰£©.
°æ¥∞∏°ø£®1£©![]() £®2£©∏√¥¨◊Ó‘Áƒİ‘Ğ¡Ë≥ø1 ±Ω¯∏𣨜¬ŒÁ17 ±≥ˆ∏𣨑Ğ∏ğøЃĞ◊Ó∂‡Õ£¡Ù16∏ˆ–° ±
£®2£©∏√¥¨◊Ó‘Áƒİ‘Ğ¡Ë≥ø1 ±Ω¯∏𣨜¬ŒÁ17 ±≥ˆ∏𣨑Ğ∏ğøЃĞ◊Ó∂‡Õ£¡Ù16∏ˆ–° ±
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫ ![]() Õ®π˝∂¡»°Õº±Ì£¨ø…“‘ø¥≥ˆ∫Ø ˝
Õ®π˝∂¡»°Õº±Ì£¨ø…“‘ø¥≥ˆ∫Ø ˝![]() µƒ÷İ∆Ğ£¨∏˘æıÀƵƒ◊Ó¥Û…Ó∂»∫Õ◊Ó–°…Ó∂»¡™¡¢∑Ω≥Ã◊È«Û≥ˆ
µƒ÷İ∆Ğ£¨∏˘æıÀƵƒ◊Ó¥Û…Ó∂»∫Õ◊Ó–°…Ó∂»¡™¡¢∑Ω≥Ã◊È«Û≥ˆ![]() £¨º¥ø…µ√µΩ∫Ø ˝
£¨º¥ø…µ√µΩ∫Ø ˝![]() µƒΩ¸À∆±Ì¥Ô Ω£ª
µƒΩ¸À∆±Ì¥Ô Ω£ª
![]() ”…“‚µ√µΩ∏√¥¨Ω¯≥ˆ∏ğ ±£¨ÀÆ…Ó”¶≤ª–°”Ğ
”…“‚µ√µΩ∏√¥¨Ω¯≥ˆ∏ğ ±£¨ÀÆ…Ó”¶≤ª–°”Ğ![]() £®√◊£©£¨”…
£®√◊£©£¨”…![]() Ω‚≥ˆ“ªÃσĞÀƅӥ۔е»”Ğ
Ω‚≥ˆ“ªÃσĞÀƅӥ۔е»”Ğ![]() µƒ ±º‰∂Œ£¨‘Ú¥¨¥”◊Ó‘Á¬˙◊„ÀÆ…ÓµΩ¥Ô
µƒ ±º‰∂Œ£¨‘Ú¥¨¥”◊Ó‘Á¬˙◊„ÀÆ…ÓµΩ¥Ô![]() µƒ ±øûÎ∏𣨥”◊ÓÕ̬˙◊„ÀÆ…Ó
µƒ ±øûÎ∏𣨥”◊ÓÕ̬˙◊„ÀÆ…Ó![]() µƒ ±øÃ≥ˆ∏ğ «◊Ó∞≤»´µƒ°£
µƒ ±øÃ≥ˆ∏ğ «◊Ó∞≤»´µƒ°£
Ω‚Œˆ£∫£®1£©”…“—÷™ ˝æı£¨“◊÷™![]() µƒ÷İ∆Ğ
µƒ÷İ∆Ğ![]() £¨‘Ú
£¨‘Ú![]() .
.
‘Ÿ”…![]() £¨µ√’Ò∑˘
£¨µ√’Ò∑˘![]() £¨
£¨
À˘“‘![]() .
.
£®2£©”…“‚£¨∏√¥¨Ω¯≥ˆ∏ğ ±£¨ÀÆ…Ó”¶≤ª–°”Ğ![]() £®√◊£©£¨
£®√◊£©£¨
À˘“‘![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
À˘“‘![]() £®
£®![]() £©£¨
£©£¨
‘ĞÕ¨“ªÃσУ¨»°![]() ªÚ1£¨À˘“‘
ªÚ1£¨À˘“‘![]() ªÚ
ªÚ![]() .
.
À˘“‘∏√¥¨◊Ó‘Áƒİ‘Ğ¡Ë≥ø1 ±Ω¯∏𣨜¬ŒÁ17 ±≥ˆ∏𣨑Ğ∏ğøЃĞ◊Ó∂‡Õ£¡Ù16∏ˆ–° ±.


 ∏ş–ß÷«ƒİøŒ ±◊˜“µœµ¡–¥∞∏
∏ş–ß÷«ƒİøŒ ±◊˜“µœµ¡–¥∞∏ Ωıæ∂—µ¡∑ºÏ≤‚æÌœµ¡–¥∞∏
Ωıæ∂—µ¡∑ºÏ≤‚æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=xlnx©Å ![]() x2©Åx+a£¨a° R
x2©Åx+a£¨a° R
£®1£©µ±a=0 ±£¨«Û∫Ø ˝f£®x£©µƒº´÷µ£ª
£®2£©»Ù∫Ø ˝f£®x£©‘Ğ∆‰∂®“”ڃД–¡Ω∏ˆ≤ªÕ¨µƒº´÷µµ„£®º´÷µµ„ «÷∏∫Ø ˝»°º´÷µ ±∂‘”¶µƒ◊‘±‰¡øµƒ÷µ£©£¨º«Œ™x1 £¨ x2 £¨ «“x1£ºx2 £Æ £®¢°£©«Ûaµƒ»°÷µ∑∂Œß£ª
£®¢¢£©»Ù≤ªµ» Ωe1+¶À£ºx1x ![]() ∫„≥…¡¢£¨«Û’˝ µ ˝¶Àµƒ»°÷µ∑∂Œß£Æ
∫„≥…¡¢£¨«Û’˝ µ ˝¶Àµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘Ğ–£‘À∂ت·…œ£¨º◊°¢““°¢±˚»˝ŒªÕ¨—ß√ø»Àæ˘¥”ï‘∂£¨Ã¯∏ş£¨«¶«Ú£¨±Í«πÀƒ∏ˆœÓƒø÷–Àʪ˙—°“ªœÓ≤Œº”±»»¸£¨ºŸ…Ë»˝»À—°œÓƒø ±ª•≤ª”∞œÏ£¨«“√ø»À—°√ø“ª∏ˆœÓƒø ±∂º «µ»ø…ƒİµƒ
£®1£©«ÛΩˆ”–¡Ω»ÀÀ˘—°œÓƒøœ‡Õ¨µƒ∏≈¬ £ª
£®2£©…ËXŒ™º◊°¢““°¢±˚»˝ŒªÕ¨—ß÷–—°Ã¯‘∂œÓƒøµƒ»À ˝£¨«ÛXµƒ∑÷≤º¡–∫Õ ˝—ß∆ĞÕ˚E£®X£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() £Æ
£Æ
£®1£©≈–∂œ∫Ø ˝![]() µƒ∆Ê≈º–‘£¨≤¢”Ë“‘÷§√˜£ª
µƒ∆Ê≈º–‘£¨≤¢”Ë“‘÷§√˜£ª
£®2£©µ±![]() ±«Û π
±«Û π![]() µƒ
µƒ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ƒ≥…˙è‘∞Ω´“ª»˝Ω«–ŒµÿøÈABCµƒ“ªΩ«APQø™±ŸŒ™ÀÆπ˚‘∞÷÷÷≤Ó ˜£¨“—÷™Ω«AŒ™120°„£¨AB£¨ACµƒ≥§∂»æ˘¥Û”Ğ200√◊£¨œ÷‘бşΩÁAP£¨AQ¥¶Ω®Œß«Ω£¨‘ĞPQ¥¶Œß÷Ò¿È∞ £Æ 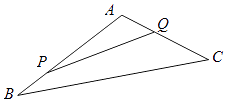
£®1£©»ÙŒß«ΩAP£¨AQ◊İ≥§∂»Œ™200√◊£¨»Á∫ŒŒßø… πµ√»˝Ω«–ŒµÿøÈAPQµƒ√ʪ˝◊Ó¥Û£ø
£®2£©“—÷™AP∂ŒŒß«Ω∏ş1√◊£¨AQ∂ŒŒß«Ω∏ş1.5√◊£¨AP∂ŒŒß«Ω‘ϺğŒ™√ø∆Ω∑Ω√◊150‘™£¨AQ∂ŒŒß«Ω‘ϺğŒ™√ø∆Ω∑Ω√◊100‘™£Æ»ÙŒßŒß«Ω”√¡À30000‘™£¨Œ »Á∫ŒŒßø… π÷Ò¿È∞ ”√¡œ◊Ó °£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ ![]() «‘≤
«‘≤![]() µƒ÷±æ∂£¨
µƒ÷±æ∂£¨ ![]() ¥π÷±‘≤
¥π÷±‘≤![]() À˘‘еƒ∆Ω√Ê£¨
À˘‘еƒ∆Ω√Ê£¨ ![]() «‘≤
«‘≤![]() …œµƒµ„£Æ
…œµƒµ„£Æ
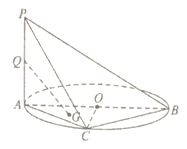
£®1£©«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©…Ë![]() Œ™
Œ™![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨ ![]() Œ™
Œ™![]() µƒ÷ÿ–ƒ£¨«Û÷§£∫
µƒ÷ÿ–ƒ£¨«Û÷§£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø![]() µƒ±ş
µƒ±ş![]() …œµƒ∏şÀ˘‘Ğ÷±œş∑Ω≥Ã∑÷±Œ™
…œµƒ∏şÀ˘‘Ğ÷±œş∑Ω≥Ã∑÷±Œ™![]() £¨
£¨ ![]() £¨∂•µ„
£¨∂•µ„![]() £¨«Û
£¨«Û![]() ±şÀ˘‘еƒ÷±œş∑Ω≥Ã.
±şÀ˘‘еƒ÷±œş∑Ω≥Ã.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘ĞÀƒ¿‚◊∂![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨∆Ω√Ê
£¨∆Ω√Ê![]() µ◊√Ê
µ◊√Ê![]() £¨
£¨![]() .
.![]() ∫Õ
∫Õ![]() ∑÷± «
∑÷± «![]() ∫Õ
∫Õ![]() µƒ÷–µ„£¨«Û÷§£∫
µƒ÷–µ„£¨«Û÷§£∫
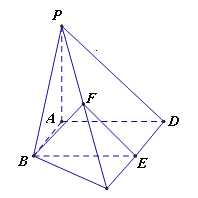
£®¢Ò£©![]() µ◊√Ê
µ◊√Ê![]() £ª
£ª
£®¢Ú£©![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®¢Û£©∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨
£¨ ![]() .
.
£®1£©Ω‚πÿ”Ğ![]() µƒ≤ªµ» Ω
µƒ≤ªµ» Ω![]() £ª
£ª
£®2£©»Ù∫Ø ˝![]() ‘Ğ«¯º‰
‘Ğ«¯º‰![]() …œµƒ÷µ”ÚŒ™
…œµƒ÷µ”ÚŒ™![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®3£©…Ë∫Ø ˝![]() £¨«Û¬˙◊„
£¨«Û¬˙◊„![]() µƒ
µƒ![]() µƒºØ∫œ.
µƒºØ∫œ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com