
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为
的长度为![]() ,在线段
,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:

记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
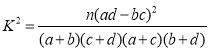
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,点A为曲线
,点A为曲线![]() 上的动点,点B在线段OA的延长线上,且满足
上的动点,点B在线段OA的延长线上,且满足![]() ,点B的轨迹为
,点B的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点C的极坐标为(2,0),求△ABC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有A,B两个投资项目,投资两项目所获得利润分别是![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系依次是:其中
(万元)的关系依次是:其中![]() 与
与![]() 平方根成正比,且当
平方根成正比,且当![]() 为4(万元)时
为4(万元)时![]() 为1(万元),又
为1(万元),又![]() 与
与![]() 成正比,当
成正比,当![]() 为4(万元)时
为4(万元)时![]() 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.
(Ⅰ)分别求出![]() ,
,![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数![]() 在区间
在区间![]() 上单调递增,且满
上单调递增,且满![]() ,给出下列判断:
,给出下列判断:
①![]() ;②
;②![]() 在
在![]() 上是减函数;③
上是减函数;③![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 在
在![]() 处取得最大值;⑤函数
处取得最大值;⑤函数![]() 没有最小值
没有最小值
其中判断正确的序号_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 上的点均在曲线
上的点均在曲线![]() 外,且对
外,且对![]() 上任意一点
上任意一点![]() ,
,![]() 到直线
到直线![]() 的距离等于该点与曲线
的距离等于该点与曲线![]() 上点的距离的最小值.
上点的距离的最小值.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,过点
,过点![]() 的直线与曲线
的直线与曲线![]() 交于另一点
交于另一点![]() ,且直线
,且直线![]() 过点
过点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
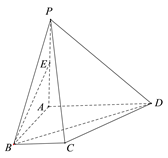
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com