
分析 (1)利用等比数列的通项公式和前n项和公式求得an,由等差数列的定义和通项公式得到bn;
(2)利用错位相减法求得数列{cn}的前N项和Tn.
解答 解:(1)设等比数列{an}的公比为q,
∵a3-3a2=0,S2=12,
∴a1q2-3a1q=0,a1+a1q=12,
解得q=3,a1=3,
∴数列{an}是等比数列,
∴an=3n.
∵bn+1-bn=2,即数列{bn}是以2为公差的等差数列,
又b1=1,
∴bn=2n-1;
(2)∵cn=an•bn=(2n-1)•3n
∵Tn=1×3+3×32+5×33+…+(2n-3)3n-1+(2n-1)3n,
∴3Tn=1×32+3×33+5×34+…+(2n-3)3n+(2n-1)3n+1,
两式相减得:-2Tn=3+2×(32+33+34+…+3n)-(2n-1)3n+1
=-6-2(n-1)3n+1,
∴Tn=3+(n-1)3n+1.
点评 本题主要考查数列通项公式和前n项和的求解,利用错位相减求和法是解决本题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $\sqrt{2+\sqrt{3}}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
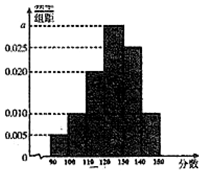 某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
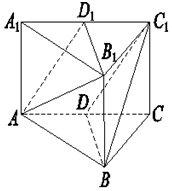 如图所示,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1中点
如图所示,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值为$\frac{2}{3}$,无最小值 | B. | 有最大值为$-\frac{1}{3}$,无最小值 | ||
| C. | 有最小值为$-\frac{1}{3}$,无最大值 | D. | 有最小值为$\frac{2}{3}$,无最大值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com