
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线
,准线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.
![]() 若
若![]() ,
,![]() ,求直线
,求直线![]() 的方程;
的方程;
![]() 若
若![]() ,点
,点![]() 为准线
为准线![]() 上任意一点,求证:直线
上任意一点,求证:直线![]() ,
,![]() ,
,![]() 的斜率成等差数列.
的斜率成等差数列.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示
年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )

A.![]() 月下旬新增确诊人数呈波动下降趋势
月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,![]() 月下旬单日治愈人数超过确诊人数
月下旬单日治愈人数超过确诊人数
C.![]() 月
月![]() 日至
日至![]() 月
月![]() 日新增确诊人数波动最大
日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在![]() 月
月![]() 日左右达到峰值
日左右达到峰值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,P是椭圆的上顶点,过点P作斜率为
,P是椭圆的上顶点,过点P作斜率为![]() 的直线l交椭圆于另一点A,设点A关于原点的对称点为B
的直线l交椭圆于另一点A,设点A关于原点的对称点为B
(1)求![]() 面积的最大值;
面积的最大值;
(2)设线段PB的中垂线与y轴交于点N,若点N在椭圆内部,求斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的左、右焦点
的左、右焦点![]() 分别作倾斜角为
分别作倾斜角为![]() 的直线
的直线![]() ,且
,且![]() 之间的距离为1.
之间的距离为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 只有一个公共点,求点
只有一个公共点,求点![]() 到直线
到直线![]() 的距离之积.
的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与y轴交于点
的图象与y轴交于点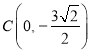 ,与x轴交于A,B两点,其中
,与x轴交于A,B两点,其中![]() ,
,![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一块边长为![]() 的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为
的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为![]() .
.

(1)若![]() ,且该容器的表面积为
,且该容器的表面积为![]() 时,在该容器内注入水,水深为
时,在该容器内注入水,水深为![]() ,若将一根长度为
,若将一根长度为![]() 的玻璃棒(粗细忽略)放入容器内,一端置于
的玻璃棒(粗细忽略)放入容器内,一端置于![]() 处,另一端置于侧棱
处,另一端置于侧棱![]() 上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
(2)求该容器的底面边长![]() 的范围,使得该容器的体积始终不大于
的范围,使得该容器的体积始终不大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
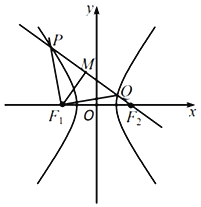
【题目】设双曲线![]() 的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且
的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com