【题目】某学校为了解学生对食堂用餐的满意度，从全校在食堂用餐的3000名学生中，随机抽取100名学生对食堂用餐的满意度进行评分．根据学生对食堂用餐满意度的评分，得到如图所示的频率分布直方图，
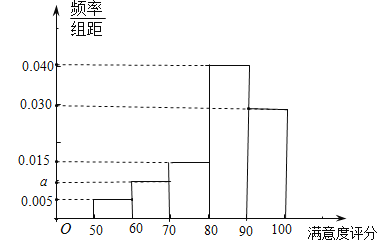
（1）求频率分布直方图中a的值及该样本的中位数
（2）规定：学生对食堂用餐满意度的评分不高于80分为“不满意”，试估计该校在食堂用餐的3000名学生中“不满意”的人数.
星级口算天天练系列答案
芒果教辅达标测试卷系列答案科目：高中数学 来源： 题型：
【题目】某高速公路隧道内设双行线公路，其截面由一段圆弧和一个长方形的三边构成（如图所示）．已知隧道总宽度
为
，行车道总宽度
为
，侧墙面高
， 
为
，弧顶高
为
．
（
）建立适当的直角坐标系，求圆弧所在的圆的方程．
（
）为保证安全，要求行驶车辆顶部（设为平顶）与隧道顶部在竖直方向上的高度之差至少要有
．请计算车辆通过隧道的限制高度是多少．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在下列向量组中，可以把向量
＝(3，2)表示出来的是( )
A. 
＝(0，0)，
＝(1，2)B. ＝(－1，2)，＝(5，－2)
C. ＝(3，5)，＝(6，10)D. ＝(2，－3)，＝(－2，3)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某保险公司决定每月给推销员确定个具体的销售目标，对推销员实行目标管理.销售目标确定的适当与否，直接影响公司的经济效益和推销员的工作积极性，为此，该公司当月随机抽取了50位推销员上个月的月销售额（单位：万元），绘制成如图所示的频率分布直方图.
（1）①根据图中数据，求出月销售额在
小组内的频率.
②根据直方图估计，月销售目标定为多少万元时，能够使70%的推销员完成任务？并说明理由.
（2）该公司决定从月销售额为
和
的两个小组中，选取2位推销员介绍销售经验，求选出的推销员来自同一个小组的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
（a＞b＞0）经过点
，且离心率为
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知A（0，b），B（a，0），点P是椭圆C上位于第三象限的动点，直线AP、BP分别将x轴、y轴于点M、N，求证：|AN||BM|为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数
与
，若存在实数
满足
，且
，则称
为
的一个
点.
(1)证明：函数
与
不存在的点；
(2)若函数
与
存在的点，求的范围；
(3)已知函数
，证明：存在正实数
，对于区间
内任意一个皆是函数的点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3，从盒中任取3张卡片.
（1）求所取3张卡片上的数字完全相同的概率;
（2）
表示所取3张卡片上的数字的中位数，求的分布列与数学期望.
（注：若三个数
满足
，则称
为这三个数的中位数）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
（
为参数），A，B是C上的动点，且满足
（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立坐标系，点D的极坐标为
.
（1）求椭圆C的极坐标方程和点D的直角坐标；
（2）利用椭圆C的极坐标方程证明
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
（1）求下表中z的值；
（2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下：94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
记这8辆轿车的得分的平均数为
，定义事件
{
，且函数
没有零点}，求事件
发生的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
