
已知数列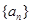 为等差数列,数列
为等差数列,数列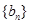 为等比数列且公比大于1,若
为等比数列且公比大于1,若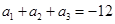 ,
,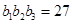 ,且
,且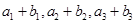 恰好是一各项均为正整数的等比数列的前三项.
恰好是一各项均为正整数的等比数列的前三项.
(1)求数列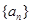 ,
,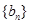 的通项公式;
的通项公式;
(2)设数列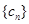 满足
满足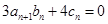
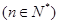 ,求
,求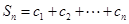 .
.
(1)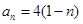 ,
,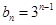 ;(2)
;(2)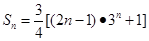 .
.
【解析】
试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识,考查思维能力和计算能力.第一问,先用等差等比数列的通项公式将已知条件中出现的所有项都展开,用
试题解析:(1)设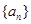 的公差为
的公差为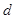 ,
,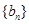 的公比为
的公比为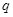 且
且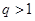 ,则
,则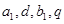 表示,从
表示,从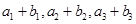 是等比数列的前三项入手,利用等比中项列表达式,可解出
是等比数列的前三项入手,利用等比中项列表达式,可解出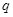 和
和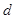 ,写出2个数列的通项公式;第二问,先将第一问的结果代入,找到
,写出2个数列的通项公式;第二问,先将第一问的结果代入,找到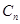 的通项公式,用错位相减法求数列的和.
的通项公式,用错位相减法求数列的和.
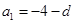 ,
,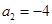 ,
,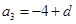 ,
,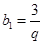 ,
,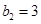 ,
,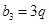 ,
,
则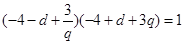 ,由于
,由于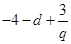 与
与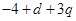 均为正整数值,
均为正整数值,
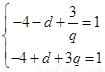 ,
,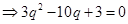 , 4分
, 4分
解得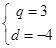 ,∴
,∴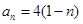 ,
,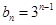 . 6分
. 6分
(2)因为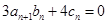
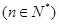 ,把
,把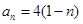 ,
,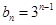 代入得:
代入得:
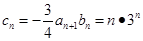 . 8分
. 8分
∴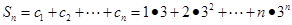 ,
,
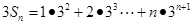 ,相减得:
,相减得:
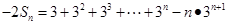
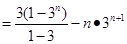
∴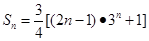 . 12分
. 12分
考点:1.等差、等比数列的通项公式;2.错位相减法;3.等比中项;4.等比数列的前n项和公式.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:2011-2012学年福建省高三上学期期中考试理科数学 题型:解答题
(13分)已知数列 为等差数列,且
为等差数列,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对任意 ,
, 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由.
恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年本溪县高二暑期补课阶段考试数学卷 题型:选择题
已知数列 为等差数列,若
为等差数列,若 且它们的前
且它们的前 项和
项和 有最大值,则使得
有最大值,则使得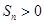 的
的 的最大值为( )
的最大值为( )
A.11 B.19 C.20 D.21
查看答案和解析>>
科目:高中数学 来源:2010-2011年黑龙江省高一下学期期中考试数学 题型:选择题
已知数列 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前 项和
项和 有最大值,则使得
有最大值,则使得 的
的 的最大值为 ( )
的最大值为 ( )
A.11 B.19 C.20 D.21
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北省高二下学期期末考试理科数学 题型:解答题
(本题满分12分)已知数列 为等差数列,
为等差数列,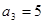 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
(1)求 、
、 的通项公式;
的通项公式;
(2)若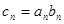 ,
, 的前
的前 项和为
项和为 ,求
,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com