
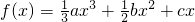 (a,b,c∈R)在点(1,f(1))处的切线斜率为
(a,b,c∈R)在点(1,f(1))处的切线斜率为 ,且a>2c>b.
,且a>2c>b.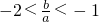 .
. ∴3a+2b+2c=0①
∴3a+2b+2c=0①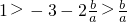 ∴
∴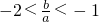
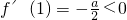 且f'(2)=a-c>0,∴f(x)在区间(1,2)内至少有一个极值点.
且f'(2)=a-c>0,∴f(x)在区间(1,2)内至少有一个极值点.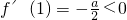 ,∴f(x)在区间(0,1)内至少有一个极值点.
,∴f(x)在区间(0,1)内至少有一个极值点.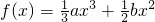 +cx(a,b,c∈R)在点(1,f(1))处的切线斜率为
+cx(a,b,c∈R)在点(1,f(1))处的切线斜率为 ,根据导数的几何意义,得到a,b,c的一个方程,由a>2c>b,根据不等式的性质寻求关于a,b的不等式;
,根据导数的几何意义,得到a,b,c的一个方程,由a>2c>b,根据不等式的性质寻求关于a,b的不等式;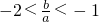 成立,难度较大,有效的考查灵活应用知识分析解决问题的能力;应用导数求函数的极值,体现了分类讨论的数学思想,属中档题.
成立,难度较大,有效的考查灵活应用知识分析解决问题的能力;应用导数求函数的极值,体现了分类讨论的数学思想,属中档题. 

科目:高中数学 来源:2011年四川省内江六中高考数学模拟试卷(文科)(解析版) 题型:解答题
 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,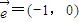 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com