
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() 的最小值为3.
的最小值为3.
【解析】试题分析:(1)利用递推公式即可得出![]() 为一个常数,从而证明数列
为一个常数,从而证明数列![]() 是等差数,再利用等差数列的通项公式即可得到
是等差数,再利用等差数列的通项公式即可得到![]() ,进而得到
,进而得到![]() ;(2)利用(1)的结论,利用“裂项求和”即可得到
;(2)利用(1)的结论,利用“裂项求和”即可得到![]() ,要使得
,要使得![]() 对于
对于![]() 恒成立,只要
恒成立,只要![]() ,即
,即![]() ,解出即可.
,解出即可.
试题解析:(1)证明:  ,
,
所以数列![]() 是等差数列,
是等差数列,
![]() ,因此
,因此![]() ,
,
由![]() .
.
(2)由![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
依题意要使![]() 对于
对于![]() ,恒成立,只需
,恒成立,只需![]() ,且
,且![]() 解得
解得![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是由正整数组成的无穷数列,该数列前
是由正整数组成的无穷数列,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() ,
, ![]() ,
, ![]() 的最小值记为
的最小值记为![]() ,
, ![]() .
.
(I)若![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,是一个周期为
,是一个周期为![]() 的数列(即对任意
的数列(即对任意![]() ,
, ![]() ),写出
),写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)设![]() 是正整数,证明:
是正整数,证明: ![]() 的充分必要条件为
的充分必要条件为![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(III)证明:若![]() ,
, ![]() ,则
,则![]() 的项只能是
的项只能是![]() 或者
或者![]() ,且有无穷多项为
,且有无穷多项为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.
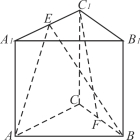
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=(1+x)m+(1+2x)n(m,n∈N*)的展开式中x的系数为11.
(1)求x2的系数取最小值时n的值;
(2)当x2的系数取得最小值时,求f(x)展开式中x的奇次幂项的系数之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 、
、![]() 是平面上左、右两个不同的定点,
是平面上左、右两个不同的定点, ![]() ,动点
,动点![]() 满足:
满足:
![]() .
.
(1)求证:动点![]() 的轨迹
的轨迹![]() 为椭圆;
为椭圆;
(2)抛物线![]() 满足:①顶点在椭圆
满足:①顶点在椭圆![]() 的中心;②焦点与椭圆
的中心;②焦点与椭圆![]() 的右焦点重合.
的右焦点重合.
设抛物线![]() 与椭圆
与椭圆![]() 的一个交点为
的一个交点为![]() .问:是否存在正实数
.问:是否存在正实数![]() ,使得
,使得![]() 的边长为连续自然数.若存在,求出
的边长为连续自然数.若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80 C.120 D.180
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com