
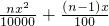 +1.
+1.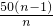 时,k值最大,此时销售额=amk,所以此时销售额也最大.
时,k值最大,此时销售额=amk,所以此时销售额也最大.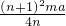 元.
元.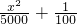 x+1,
x+1,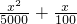 >0,
>0,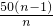 时,k值最大,此时销售额=amk,所以此时销售额也最大.
时,k值最大,此时销售额=amk,所以此时销售额也最大.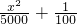 x+1,要使销售额有所增加,即k>1.从而可得-
x+1,要使销售额有所增加,即k>1.从而可得-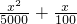 >0,解之即可.
>0,解之即可.

 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 10 |
| 2 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
 ”,0<x≤10),每月卖出的数量将减少y成,而销售金额变成原来的z倍,若y=
”,0<x≤10),每月卖出的数量将减少y成,而销售金额变成原来的z倍,若y= x,求使销售金额比原来有所增加的x的取值范围。
x,求使销售金额比原来有所增加的x的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com