
【题目】已知函数f(x)对任意的a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,且当x>0时,f(x)>1
(1)判断并证明f(x)的单调性;
(2)若f(4)=3,解不等式f(3m2﹣m﹣2)<2.
【答案】
(1)解:f(a+b)=f(a)+f(b)﹣1,
令a=b=0,
∴f(0)=f(0)+f(0)﹣1,
∴f(0)=1,
令a=x,b=﹣x,
∴f(0)=f(x)+f(﹣x)﹣1,
∴f(﹣x)=2﹣f(x),
令x1<x2,则x2﹣x1>0,
∴f(x2﹣x1)=f(x2)+f(﹣x1)﹣1
=f(x2)+2﹣f(x1)﹣1>1,
∴f(x2)>f(x1),
故函数在R上单调递增;
(2)解:f(4)=2f(2)﹣1=3,
∴f(2)=2,
∴f(3m2﹣m﹣2)<f(2),
∴3m2﹣m﹣2<2,
∴﹣1<m< ![]() .
.
【解析】(1)利用特殊值方法求出f(0)=1,和换元思想令a=x,b=﹣x,得出f(﹣x)=2﹣f(x),利用定义法判定函数的单调性;(2)根据定义得出f(2)=2,根据函数的单调性求解即可.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=ex﹣alnx(其中a∈R,e为自然常数)
①a∈R,使得直线y=ex为函数f(x)的一条切线;
②对a<0,函数f(x)的导函数f′(x)无零点;
③对a<0,函数f(x)总存在零点;
则上述结论正确的是 . (写出所有正确的结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx﹣a+2
(1)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,b的值;
(2)若b=2,a>0,解关于x的不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ﹣2lnx,a∈R.
﹣2lnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , ①求a的取值范围;
②证明:f(x2)<x2﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
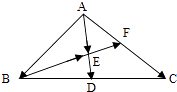
【题目】如图所示,在△ABC中,D、F分别是BC、AC的中点, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
(2)求证:B、E、F三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 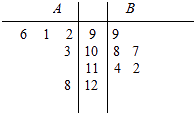
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在(﹣∞,0)∪(0,+∞)上有定义,在(0,+∞)上是增函数,f(1)=0,又知函数g(θ)=sin2θ+mcosθ﹣2m, ![]() ,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com