练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）
    ①存在点E使得直线SA⊥平面SBC
    ②平面SBC内存在直线与SA平行
    ③平面ABCE内存在直线与平面SAE平行．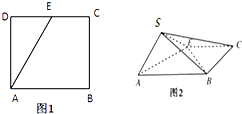

    A.0
    B.1
    C.2
    D.3

    【答案】B
    【解析】解：①当直线SA⊥平面SBC时，BC平面SBC，∴SA⊥BC；

    又AD∥BC，则SA⊥AD，这与∠SAD为锐角矛盾，∴①错误；②∵平面SBC∩直线SA=S，

    ∴平面SBC内的直线与SA相交或异面，②错误；③过点C作CF∥AE，交AB于F，∵CF平面SAE，AE平面SAE，

    由线面平行的判定定理得，CF∥平面SAE，∴③正确；

    综上，正确的命题是③．

    所以答案是：B．

    【考点精析】解答此题的关键在于理解平面与平面垂直的性质的相关知识，掌握两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某种商品价格与该商品日需求量之间的几组对照数据如表：

    价格x（元/kg）

    10

    15

    20

    25

    30

    日需求量y（kg）

    11

    10

    8

    6

    5


    （1）求y关于x的线性回归方程；
    （2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？
    参考公式：线性回归方程 ，其中 ．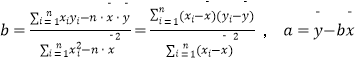

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 ，若0≤a≤1，n∈N＋且n≥2，求证：f(2x)≥2f(x).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 且an是2与Sn的等差中项．
    （1）求数列{an}的通项公式；
    （2）若 ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，点D是AB的中点．求证：

    （1）AC⊥BC1；
    （2）AC1∥平面B1CD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C所对应的边分别为a，b，c，若c（acosB﹣ b）=a2﹣b2 ．
    （1）求角A；
    （2）若a= ，求c﹣b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点p（x，y）是直线kx+y+4=0（k＞0）上一动点，PA、PB是圆C：x2+y2﹣2y=0的两条切线，A、B是切点，若四边形PACB的最小面积是2，则k的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，对a∈R，b∈（0，+∞），使得f（a）=g（b），则b﹣a的最小值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知cos（π+α）= ，且 ＜α＜π．
    （Ⅰ）求5sin（α+π）﹣4tan（3π﹣α）的值
    （Ⅱ）若0＜β＜ ，cos（β﹣α）= ，求sin（ +2β）的值．

    查看答案和解析>>

    同步练习册答案