
【题目】已知![]() ,
,![]()
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() 在其公共点
在其公共点![]() 处切线相同,求实数a的值;
处切线相同,求实数a的值;
(3)记![]() ,若函数
,若函数![]() 存在两个零点,求实数a的取值范围.
存在两个零点,求实数a的取值范围.
【答案】(1)函数的单调减区间为:![]() ;增区间为:
;增区间为:![]() (2)
(2)![]() (3)a>e
(3)a>e
【解析】
(1)根据![]() ,求导,由
,求导,由![]() 求减区间,由
求减区间,由![]() 求增区间.
求增区间.
(2)由![]() ,求导
,求导![]() ,根据
,根据![]() ,
,![]() 在其公共点
在其公共点![]() 处切线相同,由
处切线相同,由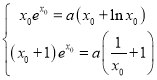 求解.
求解.
(3)易得![]() ,x>0.,求导
,x>0.,求导![]() ,令
,令![]() 得,
得,![]() ,然后分a≤0和a>0两种情况讨论求解.
,然后分a≤0和a>0两种情况讨论求解.
(1)因为![]() ,
,
所以![]() ,
,
得x=-1,
当x<-1时,![]() ;当x>-1时,
;当x>-1时,![]() .
.
所以函数的单调减区间为:![]() ;增区间为:
;增区间为:![]() .
.
(2)由![]() ,
,![]() .
.
因为点![]() 为函数
为函数![]() 的公共点,且函数
的公共点,且函数![]() 在点P处的切线相同,
在点P处的切线相同,
所以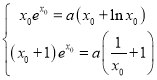 ,且
,且![]() .
.
所以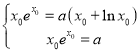 ,
,
即![]() ,
,
显然a≠0,所以![]() .
.
设![]() ,由
,由![]() 得,
得,![]() 在
在![]() 上是单调增函数,
上是单调增函数,
又![]() ,所以
,所以![]() .
.
(3)由![]() 得,
得,![]() ,x>0.
,x>0.
则![]() ,
,
令![]() 得,
得,![]() .
.
设![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上是单调增函数.
上是单调增函数.
1°当a≤0时,由x>0得,![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上是单调增函数,至多1个零点,不符,舍去.
上是单调增函数,至多1个零点,不符,舍去.
2°当a>0时,因为![]() ,
,![]() ,
,
由零点存在性定理,![]() ,
,![]() 在
在![]() 上是单调增函数且连续,
上是单调增函数且连续,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
因为![]() 存在两个零点,
存在两个零点,
所以![]() ,即
,即![]() ,从而
,从而![]() .
.
所以![]() .
.
因为![]() 在
在![]() 上是单调增函数,
上是单调增函数,
且![]() ,所以
,所以![]() ,
,
由(1)可知,![]() 在
在![]() 是单调递增,
是单调递增,
所以![]() .
.
又![]() ,
,![]() ,
,
而![]() ,易得
,易得![]() ,
,![]() ,
,
所以![]() ,
,
由零点存在性定理知,函数![]() 在
在![]() 上存在唯一一个零点,在
上存在唯一一个零点,在![]() 上存在唯一一个零点,
上存在唯一一个零点,
此时函数![]() 存在两个零点.
存在两个零点.
所以a>e.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波拉契数列,指的是这样一个数列:1,1,2,3,5,8,13,21,…,在数学上,斐波拉契数列{an}定义如下:a1=a2=1,an=an﹣1+an﹣2(n≥3,n∈N),随着n的增大,![]() 越来越逼近黄金分割
越来越逼近黄金分割![]() 0.618,故此数列也称黄金分割数列,而以an+1、an为长和宽的长方形称为“最美长方形”,已知某“最美长方形”的面积约为200平方厘米,则该长方形的长大约是( )
0.618,故此数列也称黄金分割数列,而以an+1、an为长和宽的长方形称为“最美长方形”,已知某“最美长方形”的面积约为200平方厘米,则该长方形的长大约是( )
A.20厘米B.19厘米C.18厘米D.17厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)2﹣alnx(a<0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且关于x的方程f(x)=b(b∈R)恰有三个实数根x3,x4,x5(x3<x4<x5),求证:2(x2﹣x1)>x5﹣x3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由![]() 和
和![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,将
,将![]() 和
和![]() 分别沿着
分别沿着![]() ,
,![]() 折起,使得
折起,使得![]() 与
与![]() 重合于点B,G为
重合于点B,G为![]() 的中点,如图2.
的中点,如图2.
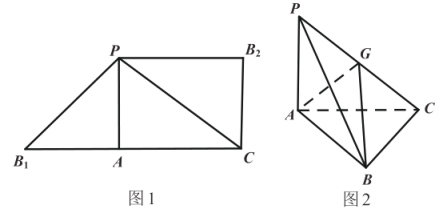
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求点C到平面
,求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() (
(![]() )的焦点为F,过F且斜率为1的直线与C交于A,B两点,
)的焦点为F,过F且斜率为1的直线与C交于A,B两点,![]() .
.
(1)求C的方程;
(2)过点![]() 的直线l交C于点M,N,点Q为
的直线l交C于点M,N,点Q为![]() 的中点,
的中点,![]() 轴交C于点R,且
轴交C于点R,且![]() ,证明:动点T在定直线上.
,证明:动点T在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com