
【题目】圆![]() 的方程为:
的方程为:![]() ,
,![]() 为圆上任意一点,过
为圆上任意一点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,及直线
的最大值,及直线![]() 的方程.
的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
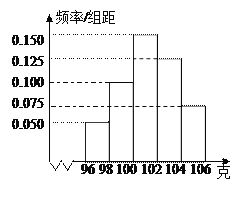
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中,原文记载如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”其核心思想编译成如示框图,若输入的![]() ,
,![]() 分别为45,63,则输出的
分别为45,63,则输出的![]() 为( )
为( )
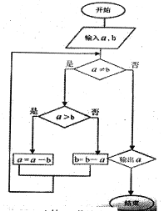
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中,原文记载如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”其核心思想编译成如示框图,若输入的![]() ,
,![]() 分别为45,63,则输出的
分别为45,63,则输出的![]() 为( )
为( )
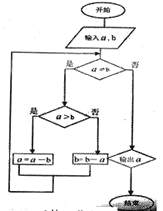
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,AB∥CD,AB![]() ,E为PC中点.
,E为PC中点.
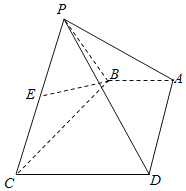
(Ⅰ)证明:BE∥平面PAD;
(Ⅱ)若AB⊥平面PBC,△PBC是边长为2的正三角形,求点E到平面PAD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com