
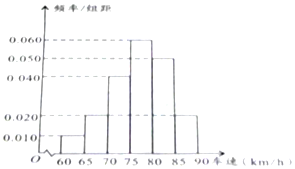
 ��˫�ڡ��ڼ䣬���ٹ�·�����϶࣬ij���鹫˾��һ���������������µ�С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ��������������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�km/h���ֳ����Σ�[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
��˫�ڡ��ڼ䣬���ٹ�·�����϶࣬ij���鹫˾��һ���������������µ�С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ��������������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�km/h���ֳ����Σ�[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ֪[75��80����Ӧ��С������ߣ��ɴ��������40��С���������ٵ���������Ƶ�ʷֲ�ֱ��ͼ���[60��75����Ӧ��Ƶ��Ϊ0.35��[75��80����Ӧ��Ƶ��Ϊ0.3���ɴ��������λ���Ĺ���ֵ��
��2��������[60��70����Ƶ��Ϊ0.15���Ӷ�������[60��70���ڵij�����6�������г�����[60��65���ڵij�����2����������[65��70���ڵij�����4�����ɴ�������ӳ�����[60��70���ڵij������γ�ȡ2����������[65��70���ڵij���ǡ��һ���ĸ��ʣ�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ֪[75��80����Ӧ��С������ߣ�
����40��С���������ٵ�����Ϊ��$\frac{75+80}{2}$=77.5��km/h����
��Ƶ�ʷֲ�ֱ��ͼ֪[60��75����Ӧ��Ƶ��Ϊ��
��0.010+0.020+0.040����5=0.35��
[75��80����Ӧ��Ƶ��Ϊ��0.060��5=0.3��
����λ���Ĺ���ֵΪ��$75+\frac{��0.5-0.35��}{0.3}��5$=77.5��km/h����
��2��������[60��70����Ƶ��Ϊ��0.010+0.020����5=0.15��
�����[60��70���ڵij�����0.15��40=6����
���г�����[60��65���ڵij����У�0.010��5��40=2����
������[65��70���ڵij����У�0.020��5��40=4����
��ӳ�����[60��70���ڵij������γ�ȡ2����
�����¼�����n=${C}_{6}^{2}=15$��
������[65��70���ڵij���ǡ��һ�������Ļ����¼�����m=${C}_{4}^{1}{C}_{2}^{1}$=8��
�����[65��70���ڵij���ǡ��һ���ĸ���p=$\frac{m}{n}$=$\frac{8}{15}$��
���� ���⿼����������λ������������ʵ����ǻ����⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | cos��=2cos�� | B�� | cos2��=2cos2�� | C�� | cos2��=2cos2�� | D�� | cos2��=-2cos2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | $��1��1+\sqrt{2}��$ | C�� | $��1��\sqrt{3}��$ | D�� | $��1-\sqrt{2}��1+\sqrt{2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 150�� | C�� | 60�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | 2 | C�� | $\frac{5}{3}$ | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com