【题目】我国在北宋年间（公元1084年）第一次印刷出版了《算经十书》，即贾宪的《黄帝九章算法细草》，刘益的《议古根源》，秦九韶的《数书九章》，李冶的《测圆海镜》和《益古演段》，杨辉的《详解九章算法》、《日用算法》和《杨辉算法》，朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰，其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.哈三中图书馆中正好有这十本书，现在小张同学从这十本书中任借三本阅读，那么他借到的三本书中书名中恰有一个“算”字的概率为______.
科目：高中数学 来源： 题型：
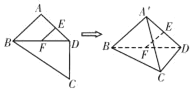
【题目】如图，平面四边形
中，E，F是
，
中点，
，
，
，将
沿对角线折起至
，使平面
平面
，则四面体
中，下列结论不正确的是（ ）
A.
平面
B.异面直线
与
所成的角为90°
C.异面直线
与
所成的角为60°D.直线与平面所成的角为30°
查看答案和解析>>
科目：高中数学 来源： 题型：
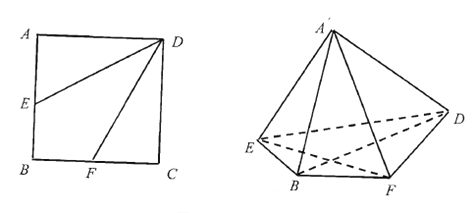
【题目】如图，正方形
的边长为4，点
， 
分别为
， 
的中点，将
， 
，分别沿
， 
折起，使
， 
两点重合于点
，连接
.
（1）求证： 
平面
；
（2）求
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的上顶点为
，左，右焦点分别为
，
，
的面积为
，直线
的斜率为.
为坐标原点.
（1）求椭圆的方程；
（2）设过点
的直线
与椭圆交于点
（不在
轴上），垂直于的直线与交于点
，与
轴交于点
.
，且
，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召，实施网络授课，为检验学生上网课的效果，高三学年进行了一次网络模拟考试.全学年共1500人，现从中抽取了100人的数学成绩，绘制成频率分布直方图（如下图所示）.已知这100人中
分数段的人数比
分数段的人数多6人.
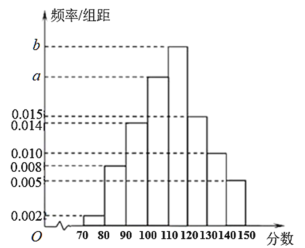
（1）根据频率分布直方图，求a，b的值，并估计抽取的100名同学数学成绩的中位数；
（2）现用分层抽样的方法从分数在
，
的两组同学中随机抽取6名同学，从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言，求这2名同学的分数不在同一组内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的普通方程为
，以原点
为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（I）求的参数方程与的直角坐标方程；
（II）射线
与交于异于极点的点
,与的交点为
,求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
大学生是国家的未来，代表着国家可持续发展的实力，能够促进国家综合实力的提高.据统计，2016年至2020年我国高校毕业生人数y(单位：万人)的数据如下表：
年份 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代号x | 16 | 17 | 18 | 19 | 20 |
高校毕业生人数y(单位：万人) | 765 | 795 | 820 | 834 | 874 |
（1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性的强弱.
(已知：
，则认为y与x线性相关性很强；
，则认为y与x线性相关性一般；
，则认为y与x线性相关性较弱)
（2）求y关于x的线性回归方程，并预测2022年我国高校毕业生的人数(结果取整数).
参考公式和数据：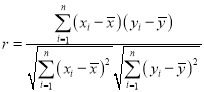
，
，
，
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4―4：坐标系与参数方程]
在直角坐标系xOy中，曲线C的参数方程为
（θ为参数），直线l的参数方程为
.
（1）若a=1，求C与l的交点坐标；
（2）若C上的点到l的距离的最大值为
，求a.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的长轴长为
，且离心率为
.
（1）求椭圆
的标准方程；
（2）设椭圆的左焦点为
，点
是椭圆与
轴负半轴的交点，经过的直线
与椭圆交于点
，经过且与平行的直线与椭圆交于点
，若
，求直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
