
叙述并证明正弦定理.
 ,运用向量法表示来证明,或者借助于三角函数的性质来证明。
,运用向量法表示来证明,或者借助于三角函数的性质来证明。
解析试题分析:
证明(向量法):
(1)当 为直角三角形时,
为直角三角形时, .
.
由锐角三角函数的定义,有 ,所以
,所以 .
.
又 ,所以
,所以 .
.
(2)当 为锐角三角形时,如图示
为锐角三角形时,如图示
过点 作单位向量
作单位向量 垂直于
垂直于 ,则
,则 ,
, .
.
又由图知, ,为了与图中有关的三角函数建立联系,对上面向量等式的两边同取与向量
,为了与图中有关的三角函数建立联系,对上面向量等式的两边同取与向量 的数量积运算,得到:
的数量积运算,得到: ,所以
,所以 ,即
,即
所以 .
.
同理,过点 作与
作与 垂直的单位向量
垂直的单位向量 ,可得
,可得 .所以
.所以 .
.
(2)当 为钝角三角形时,不妨设
为钝角三角形时,不妨设 ,如图示
,如图示
过点 作与
作与 垂直的单位向量
垂直的单位向量 ,
, ,
, .
.
同样,可证得 .因此,对于任意三角形均有
.因此,对于任意三角形均有 .
.
注:还可运用三角函数定义法证明或者等面积法证明。
考点:正弦定理
点评:掌握运用向量的方法来证明正弦定理,简单明了,感受向量的几何运用,属于基础题。


科目:高中数学 来源: 题型:解答题
已知函数
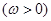 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中, ,
, ,
, 为
为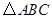 的内角
的内角 的对边,
的对边,
且满足 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,设
,设 ,
, ,
, ,求四边形
,求四边形 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?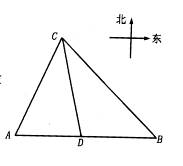
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com